11551. x1 + x2 + … + xk = n
(2)
Given values of k and n, find
the number of nonnegative integral solutions for the equation
x1 + x2 + ...+ xk = n
Input. Two positive integers k and n (k ≤ n ≤ 100).
Output. Print the number of nonnegative integral solutions for
the given equation. It is known that the answer is no more than 1018.
|
Sample
input |
Sample
output |
|
3 4 |
15 |
SOLUTION
combinatorics
Algorithm analysis
Consider a
sequence of n + k – 1 positions. In n positions we should place 1. In k – 1 positions we should place the ‘+’ symbol (to obtain k terms).
Any arrangement
of 1s and ‘+’ signs among these positions will
correspond to some solution of the given equation. For example, consider some solutions of the equation x1 + x2 + x3 = 4 (4 ones and 2 plus signs):
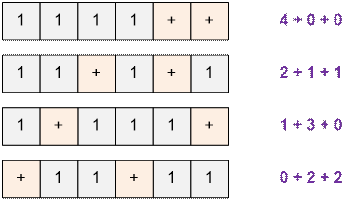
We should insert k – 1 plus signs
into n + k – 1 positions. This can be done in ![]() ways.
ways.
Example
Consider the equation x1 + x2 + x3 = 4. Its solutions are:
·
(4, 0, 0) and its 3 permutations;
·
(3, 1, 0) and its 6 permutations;
·
(2, 2, 0) and its 3 permutations;
·
(2, 1, 1) and its 3 permutations;
There are 3 + 6 + 3 + 3 = 15 solutions.
Algorithm implementation
The
Cnk function computes the value of the binomial
coefficient ![]() .
.
long long Cnk(long long k, long long n)
{
long long res = 1;
if (k > n - k) k = n - k;
for (long long i = 1; i <= k; i++)
res = res * (n - i + 1) / i;
return res;
}
The main part of the program. Read the input data.
scanf("%lld %lld", &k, &n);
Compute
and print the answer – the value of ![]() .
.
res = Cnk(k - 1, n +
k - 1);
printf("%lld\n", res);
Python implementation
import math
Read the input data.
k, n = map(int,input().split())
Compute
and print the
answer – the value of ![]() .
.
res = math.comb(n + k - 1, k - 1)
print(res)