11602. Two round dances

One day n people (n is even) met on a plaza and made two round dances. Find the number of ways n people can make two round dances if each round dance consists of exactly n / 2 people. Each person should belong to exactly one of these two round dances.

Round dance is a dance circle consisting of 1 or more people. Two round dances are indistinguishable (equal) if one can be transformed to another by choosing the first participant. For example, round dances [1, 3, 4, 2], [4, 2, 1, 3] and [2, 1, 3, 4] are indistinguishable.

Input. One even integer n (2 ≤ n ≤ 20).

Output. Print the number of ways to make two round dances. It is guaranteed that the answer fits in the 64-bit integer data type.

Sample input	Sample output
4	3

SOLUTION

combinatorics

Algorithm analysis

First, we should select n / 2 people for the first circle dance. This can be done in ways. Let’s count the number of ways to arrange people within one circle dance. Fix the person who will be first, after which the remaining n / 2 – 1 people can be arranged in any order, namely (n / 2 – 1)! ways. The number of ways to form two circle dances is:

* (n / 2 – 1)! * (n / 2 – 1)! / 2

The division by 2 is necessary so that we do not distinguish between pairs of circle dances (x, y) and (y, x). For example, for n = 4, the divisions into circle dances ([1, 2], [3, 4]) and ([3, 4], [1, 2]) are considered the same.

Simplifying the given formula, we get the answer:

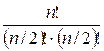* (n / 2 – 1)! * (n / 2 – 1)! / 2 =

= =

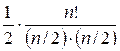Example

For example, for n = 4 the number of ways is 3:

· One round dance – [1, 2], another – [3, 4];

· One round dance – [2, 4], another – [3, 1];

· One round dance – [4, 1], another – [3, 2].

According to the formula for n = 4, the answer is

= = 3

Let’s construct all distinguishable circle dances for n = 4. We place participant 1 in the first position. In the remaining three positions, any permutation of the other three participants can be placed.

By rotating any of these arrangements in a circle, we can obtain indistinguishable circle dances. For example, the following arrangements are indistinguishable (consider the cyclic shifts of the last permutation):

[1, 4, 3, 2], [2, 1, 4, 3], [3, 2, 1, 4], [4, 3, 2, 1]

There are 4! = 24 circle dances with 4 participants. However, the number of distinguishable circle dances for n = 4 is 3! = 6.

Algorithm realization

The fact function computes the factorial of the number n.

long long fact(int n)

{

long long res = 1;

for (int i = 2; i <= n; i++)

res *= i;

return res;

}

The main part of the program. Read the input value of n.

scanf("%d", &n);

Compute and print the result.

res = 2 * fact(n - 1) / n;

printf("%lld\n", res);

Python realization

The fact function computes the factorial of the number n.

def fact(n):

res = 1

for i in range(2, n + 1):

res *= i

return res

The main part of the program. Read the input value of n.

n = int(input())

Compute and print the result.

res = 2 * fact(n - 1) // n

print(res)