11664. Array partition

Given an integer array of 2n integers.

Group these integers into n pairs (a₁, b₁), (a₂, b₂), ..., (a_n, b_n) such that the sum of min(a_i, b_i) for all i is maximized.

Input. The first line contains one number n (n ≤ 10⁵). The second line contains 2n integers, each no more than 10⁵ by absolute value.

Output. Print the maximum possible value of the sum

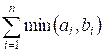
Sample input	Sample output
2 4 1 3 2	4

SOLUTION

greedy

Algorithm analysis

Let x₁ ≤ x₂ ≤ … x_2n be a sorted array. Pair the elements as follows: (x₁, x₂), (x₃, x₄), …, (x_2n-1, x_2n). Then the desired sum is equal to the sum of the elements of the sorted array with odd indices:

min(x₁, x₂) + min(x₃, x₄) + … + min(x_2n-1, x_2n) = x₁ + x₃ + … + x_2n-1

Example

The sorted array looks like this: (1, 2, 3, 4).

Let’s pair the numbers: (1, 2), (3, 4). Then the desired sum will be equal to

min(1, 2) + min(3, 4) = 1 + 3 = 4

Algorithm realization

Read the input data.

scanf("%d", &n);

v.resize(2 * n);

for (i = 0; i < 2 * n; i++)

scanf("%d", &v[i]);

Sort the array.

sort(v.begin(), v.end());

In the variable s we compute the desired sum.

s = 0;

for (i = 0; i < 2 * n; i += 2)

s += v[i];

Print the answer.

printf("%lld\n", s);