11719. Reduce the array
Given an array of n integers
and an integer k. Find the minimum cost to reduce the array to a
single element. You can perform the following operation any number of times:
·
Choose
any pair of consecutive elements ai and ai+1, and replace them
with (ai
+ ai+1). The cost of this operation is k * (ai + ai+1).
Input. The first line contains two integer n and
k (n, k ≤ 100). The second line contains n integers
a1, a2, …, an
(0 ≤ ai ≤ 100).
Output. Print the minimum cost to reduce the array to a
single element.
|
Sample input 1 |
Sample output
1 |
|
3 2 1 2 3 |
18 |
|
|
|
|
Sample input 2 |
Sample output
2 |
|
4 3 4 5 6 7 |
132 |
SOLUTION
dynamic programming
Algorithm analysis
Let f(i, j) represent the minimum cost
to reduce the subarray [ai,
…, aj] to a
single element. This value will be stored in the cell dp[i][j].
Obviously, f(i, i) = 0.
From the problem statement, it follows that
f(i, i + 1) = k * (ai + ai+1)
Now, let’s compute f(i, i + 2). Reducing three
numbers into one can be done in two ways:
·
Merge ai and ai+1 with a cost of k * (ai + ai+1), then merge ai + ai+1 and ai+2 at a cost of k * (ai
+ ai+1 + ai+2).
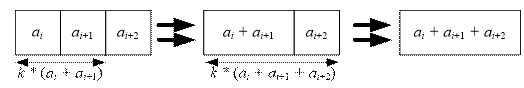
·
Merge ai+1 and ai+2 with a cost of k * (ai+1 + ai+2), then merge ai and ai+1 + ai+2 at a cost of k * (ai + ai+1
+ ai+2).
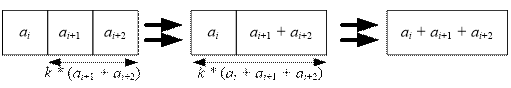
Thus f(i, i + 2) =
min(k * (ai + ai+1) + k * (ai
+ ai+1 + ai+2), k * (ai+1
+ ai+2) + k * (ai + ai+1
+ ai+2))
Now, let’s consider
calculating the value of f(i, j). To reduce the subarray [ai, …, aj] to a single element equal to ai + …+ aj, we need to choose some value p (i ≤
p < j). Then, recursively solve the problem for the subarrays [ai,
…, ap] and [ap+1,
…, aj], and finally merge the
elements ai + … + ap and ap+1 + … + aj. The value of p should be chosen in such a way
that the total transformation cost is minimized:
f(i, j) = ![]()
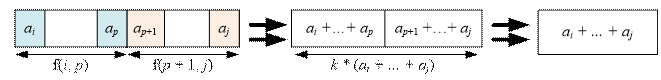
For efficient computation
of sums ai + …+ aj, use a prefix sum array pref, where
pref[i] = a1 + …+ ai,
so that ai + …+ aj = pref[j] – pref[i – 1] .
Algorithm implementation
Let’s
declare constants and arrays.
#define MAX 101
#define INF 0x3F3F3F3F
int dp[MAX][MAX], a[MAX],
pref[MAX];
The function f(i, j) returns the
minimum cost to transform the subarray [ai,
…, aj] into a
single element.
int f(int i, int j)
{
if (dp[i][j] == INF)
for (int p = i; p
< j; p++)
dp[i][j] = min(dp[i][j], f(i, p) +
f(p + 1, j) +
(pref[j] - pref[i - 1])
* k);
return dp[i][j];
}
The
main part of the program. Read the input data.
scanf("%d %d", &n, &k);
memset(dp,
0x3F, sizeof(dp));
for (i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
dp[i][i] = 0;
Compute
the array of prefix sums.
pref[i] = pref[i - 1] + a[i];
}
Compute
and print the answer.
printf("%d\n", f(1, n));
Python implementation
Let’s
declare the constant for infinity.
INF = float('inf')
The function f(i, j) returns the
minimum cost to transform the subarray [ai,
…, aj] into a
single element.
def f(i, j):
if dp[i][j] == INF:
for p in range(i, j):
dp[i][j] = min(dp[i][j], f(i, p) + f(p + 1, j) +
(pref[j] - pref[i - 1]) * k)
return dp[i][j]
The
main part of the program. Read the input data.
n, k = map(int, input().split())
a = [0] + list(map(int, input().split()))
Compute
the array of prefix sums.
pref = [0] * (n + 1)
for i in range(1, n + 1):
pref[i] = pref[i - 1] + a[i]
Initialize
the dp array.
dp = [[INF] * (n + 1) for
_ in range(n + 1)]
for i in range(1, n + 1):
dp[i][i] = 0
Compute
and print the answer.
print(f(1, n))