11720. Jim and the Skyscrapers

Given an array h₁, h₂, ..., h_n. Count the number of pairs of indices (i, j) (1 ≤ i < j ≤ n) such that the following conditions hold: h_i = h_j and .

Input. The first line contains one integer n (1 ≤ n ≤ 3 ⋅ 10⁵). The second line contains n integers h₁, h₂, ..., h_n (1 ≤ h_i ≤ 10⁶).

Output. Print the number of pairs of indices that satisfy the given conditions.

Sample input 1	Sample output 1
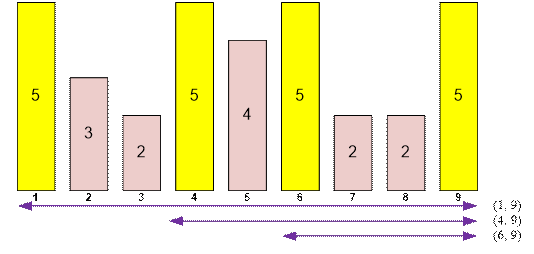
6 3 2 1 2 3 3	4
Sample input 2	Sample output 2
10 5 3 5 3 2 3 1 3 5 5	9

SOLUTION

stack

Algorithm analysis

Imagine that we are building “walls” out of blocks of the same height.
A pair (i, j) forms a “corridor” if there is no taller block between these walls.

To solve the problem, we’ll use a monotone stack. The stack stores pairs (value, count):

· value – the height of the wall (the value h[i]).

· count – the number of consecutive elements of this height that have already appeared and can form pairs with future elements of the same height.

That is:

· For each “block of identical numbers”, we remember only two parameters: the number itself and how many times it has appeared consecutively so far.

· When a new element appears, we can immediately determine how many pairs it forms: this number is exactly count for the element at the top of the stack.

For example, let the current number be a = 5, and suppose it has already appeared 3 times (that is, the current occurrence of a = 5 is the fourth one). Assume that between all these occurrences of a there are only smaller elements. Then the number of new index pairs (i, j), where j is the current index and the condition h_i = h_j = a holds, will be 3.

When processing the next number h_i:

· If the number at the top of the stack is less than h_i, remove it from the stack.

· If the number at the top of the stack is equal to h_i and it has appeared previously x times, increase the target count of index pairs by x and update the number of occurrences of h_i to x + 1.

· If the stack is empty or the number at the top of the stack is greater than h_i, push the pair (h_i, 1) onto the stack. This means that the current value h_i appears for the first time (it may have appeared earlier in the input sequence but was removed from the stack due to a larger element).

Example

Consider the first test case.

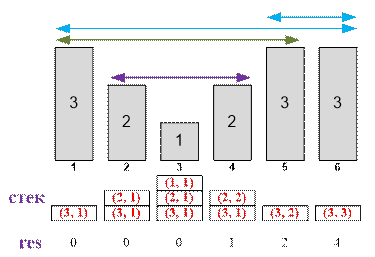
Algorithm implementation

Read the input data.

scanf("%d", &n);

vector<int> v(n);

for (i = 0; i < n; ++i)

scanf("%d", &v[i]);

Store the number of found index pairs in the variable res.

res = 0;

Declare a stack of pairs.

stack<pair<int, int>> st;

Process all the numbers of the array sequentially.

for (i = 0; i < v.size(); i++)

{

While the number at the top of the stack is less than v[i], remove it from the stack.

while (!st.empty() && st.top().first < v[i])

st.pop();

If the number at the top of the stack is equal to v[i] and it has appeared previously x times (the value x is stored in st.top().second), increase the answer res by x. Then update the number of occurrences of v[i] to x + 1.

if (!st.empty() && v[i] == st.top().first)

{

res += st.top().second;

st.top().second += 1;

}

else

If v[i] appears for the first time, push the pair (v[i], 1) onto the stack.

st.push({ v[i], 1 });

}

Print the answer.

printf("%lld\n", res);