11721. Subarray sums 1

Given an array of n positive integers, find the number of subarrays whose sum is equal to x.

Input. The first line contains the size of the array n (1 ≤ n ≤ 2 * 10⁵) and the target sum x (1 ≤ x ≤ 10⁹). The next line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹) – the contents of the array.

Output. Print the required number of subarrays.

Sample input	Sample output
5 7 2 4 1 2 7	3

SOLUTION

two pointers

Algorithm analysis

Let’s implement a sliding window using two pointers, i and j. For each fixed i = 1, 2, …, expand the interval [i … j] as much as possible so that the sum of its elements does not exceed x. In other words, for each i, search for the largest possible j such that the sum of elements in the interval [i … j] does not exceed x, while the sum of elements in the interval [i … j + 1] exceeds x.

Let s be the sum of numbers in the interval [i … j]. If s + a[j + 1] ≤ m, expand the interval to [i … j + 1]. Otherwise, shrink it to [i + 1 … j]. Count the number of intervals with a sum of x.

Example

Let’s examine the movement of the pointers for the given example.

1. i = 0, j moves forward until the sum of the numbers in the interval [i … j] exceeds x = 7. We stop at the interval [0 … 2], since the sum of the numbers in it is 7, while in the interval [0 … 3], the sum of the numbers is already 9.

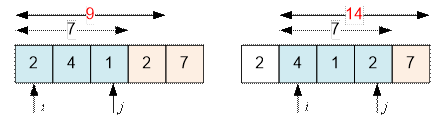
2. i = 1, j moves forward to 3. The sum of the numbers in the interval [1 … 3] is 7, while in the interval [1 … 4], it is already 14.

3. i = 2, the considered interval is [2 … 3]. The sum of the numbers in it is 3, but we cannot move the index j forward because the sum of the numbers in the interval [2 … 4] is 10, which is greater than x = 7.

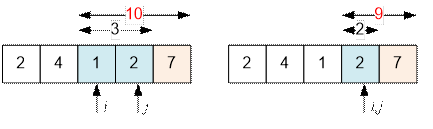
4. i = 3, the considered interval is [3 … 3]. The sum of the numbers in it is 2, but we cannot move the index j forward because the sum of the numbers in the interval [3 … 4] is 9, which is greater than x = 7.

5. i = 4, the considered interval is [4 … 4]. The sum of the numbers in it is 7.

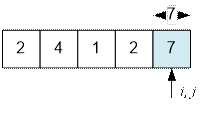
The number of subarrays with a sum of x = 7 is 3. They start at indices 0, 1, and 4.

Algorithm realization

Declare an array.

#define MAX 200001

long long a[MAX];

Read the input data.

scanf("%d %lld", &n, &x);

for (i = 0; i < n; i++)

scanf("%lld", &a[i]);

Initially, set the current interval [i … j] = [0; 0]. The sum of the numbers in this interval is s = 0.

s = j = 0;

For each value of i, sequentially process the intervals [i … j].

for (i = 0; i < n; i++)

{

For the fixed left end i of the interval [i … j], search for the largest j such that the sum of elements in this interval does not exceed x.

while ((j < n) && (s + a[j] <= x)) s += a[j++];

If the sum of the numbers s in the current interval [i … j] equals x, increase the desired subarray count cnt by 1.

if (s == x) cnt++;

Recompute the sum s for the interval [i + 1 … j].

s -= a[i];

}

Print the answer.

printf("%lld\n", cnt);