11722. Разрезание прямоугольника

Дан прямоугольник размером a × b. Ваша задача – разрезать его на квадраты. За один ход можно выбрать один из прямоугольников и разрезать его на два новых прямоугольника так, чтобы все длины сторон оставались целыми числами. Определите наименьшее количество ходов, которое потребуется для этого.

Вход. Два целых числа a и b (1 ≤ a, b ≤ 500).

Выход. Выведите минимальное количество ходов, необходимое для разрезания прямоугольника на квадраты.

Пример входа 1	Пример выхода 1
3 5	3
Пример входа 2	Пример выхода 2
5 10	1

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть f(a, b) – наименьшее количество ходов, за которое прямоугольник размером a × b можно разрезать на квадраты. Будем хранить это значение в ячейке dp[a][b].

Если прямоугольник уже является квадратом (a = b), разрезы не требуются, поэтому f(a, a) = 0.

Прямоугольник a × b можно разрезать либо вертикальным, либо горизонтальным разрезом. Рассмотрим сначала вертикальный разрез.

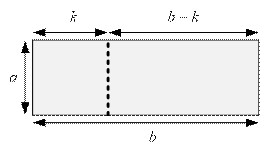
При вертикальном разрезе прямоугольник a × b делится на два прямоугольника: a × k и a × (b – k). Чтобы полученные прямоугольники были невырожденными, должно выполняться условие 1 ≤ k < b. Затем рекурсивно решаем задачу для каждого из этих двух прямоугольников и добавляем 1 к результату, так как мы сделали один вертикальный разрез. При этом выбираем такое k, для которого сумма f(a, k) + f(a, b – k) + 1 наименьшая:

f(a, b) =

Для случая горизонтального разреза получаем аналогичную формулу:

f(a, b) =

Остаётся выбрать минимальное значение среди этих двух вариантов.

Пример

В первом тесте требуется выполнить 3 разреза:

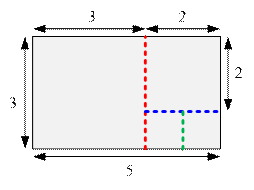
· Первым разрезом прямоугольник 3 × 5 разделяется на 3 × 3 и 2 × 3;

· Вторым разрезом прямоугольник 2 × 3 разделяется на 2 × 2 и 2 × 1;

· Третьим разрезом прямоугольник 2 × 1 разделяется на 1 × 1 и 1 × 1;

Реализация алгоритма

Объявим константы и рабочий массив.

#define MAX 501

#define INF 0x3F3F3F3F

int dp[MAX][MAX];

Функция f(a, b) возвращает наименьшее количество ходов, за которое прямоугольник размером a × b можно разрезать на квадраты.

int f(int a, int b)

{

Если прямоугольник уже является квадратом (a = b), разрезы не требуются.

if (a == b) return 0;

Если значение f(a, b) еще не вычислено (dp[a][b] = ∞), то вычисляем его.

if (dp[a][b] == INF)

{

Выполняем все возможные вертикальные разрезы.

for (int k = 1; k < b; k++)

dp[a][b] = min(dp[a][b], f(a, k) + f(a, b - k) + 1);

Выполняем все возможные горизонтальные разрезы.

for (int k = 1; k < a; k++)

dp[a][b] = min(dp[a][b], f(k, b) + f(a - k, b) + 1);

}

Возвращаем результат f(a, b) = dp[a][b].

return dp[a][b];

}

Основная часть программы. Читаем размеры прямоугольника a и b.

scanf("%d %d", &a, &b);

Вычисляем и выводим ответ.

memset(dp, 0x3F, sizeof(dp));

printf("%d\n", f(a, b));