11722. Rectangle cutting
A rectangle of size a × b is given. Your task is to cut it
into squares. In one move, you can select one of the rectangles and split it
into two new rectangles so that all side lengths remain integers. Determine the
minimum number of moves required to complete this task.
Input. Two integers a and b (1 ≤ a, b ≤
500).
Output. Print the minimum number of moves required to cut the
rectangle into squares.
|
Sample input 1 |
Sample output
1 |
|
3 5 |
3 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
5 10 |
1 |
SOLUTION
dynamic programming
Algorithm analysis
Let f(a, b) be the minimum number of moves required
to cut a rectangle of size a × b into squares. We’ll store this value in the cell dp[a][b].
If the rectangle
is already a square (a = b), no cuts are needed, so f(a, a) = 0.
A rectangle a × b
can be cut either vertically or horizontally. Let’s first consider a vertical cut.
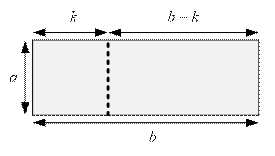
With a vertical cut, the rectangle a × b is divided into two rectangles: a × k and a × (b – k). For the resulting rectangles to be
non-degenerate, the condition 1 ≤ k < b must hold. Then recursively solve the problem for each of these two
rectangles and add 1 to the result, as we made one vertical cut. We choose such
a k that minimizes the sum f(a, k) + f(a, b – k)
+ 1:
f(a, b) = ![]()
For a horizontal cut, we
get a similar formula:
f(a, b) = ![]()

It remains to choose the
minimum value among these two options.
Example
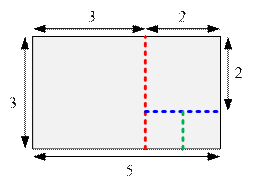
In the first test, 3 cuts are required:
·
The
first cut divides the 3 × 5 rectangle
into 3 ×
3 and 2 × 3;
·
The
second cut divides the 2 × 3 rectangle
into 2 ×
2 and 2 × 1;
·
The
third cut divides the 2 × 1 rectangle
into 1 ×
1 and 1 × 1;
Algorithm implementation
Let’s
declare constants and the array.
#define MAX 501
#define INF 0x3F3F3F3F
int dp[MAX][MAX];
The
function f(a, b) returns the minimum number of moves required to cut a rectangle
of size a × b into squares.
int f(int a, int b)
{
If
the rectangle is already a square (a = b), no cuts are needed.
if (a == b) return 0;
If
the value of f(a, b)
is not computed (dp[a][b] = ∞), compute it.
if (dp[a][b] == INF)
{
Perform
all possible vertical cuts.
for (int k = 1;
k < b; k++)
dp[a][b] = min(dp[a][b], f(a, k) +
f(a, b - k) + 1);
Perform
all possible horizontal cuts.
for (int k = 1;
k < a; k++)
dp[a][b] = min(dp[a][b], f(k,
b) + f(a - k, b) + 1);
}
Return
the result f(a, b) = dp[a][b].
return dp[a][b];
}
The
main part of the program. Read the dimensions of the rectangle a and b.
scanf("%d %d", &a, &b);
Compute
and print the answer.
memset(dp, 0x3F, sizeof(dp));
printf("%d\n", f(a, b));