11724. Зараженное
дерево
Задано бинарное дерево – ациклический
связный неориентированный граф, содержащий n вершин и n – 1 ребро.
Каждая вершина имеет степень не больше 3, а корнем является вершина с
номером 1, причем её степень не превышает 2.
К сожалению, корень дерева
заражён. Следующий процесс повторяется n раз:
·
Хусейн либо выбирает ещё не заражённую (и не удалённую) вершину и удаляет
её вместе со всеми инцидентными ей рёбрами, либо ничего не предпринимает.
·
После этого заражение распространяется на каждую вершину, соединённую
ребром с уже заражённой вершиной (все ранее заражённые вершины остаются
заражёнными).
Помогите Хусейну определить,
какое максимальное количество вершин он может спасти от заражения (учтите, что
удалённые вершины не считаются спасёнными).
Вход. Первая строка содержит количество
вершин дерева n (2 ≤ n ≤ 3 * 105).
Каждая из следующих n – 1 строк
содержит два числа ui и vi (1 ≤ ui,
vi ≤ n), обозначающих ребро дерева.
Гарантируется, что граф является
бинарным деревом с корнем в вершине 1.
Выход. Выведите одно целое число – количество
спасенных вершин.
|
Пример входа 1 |
Пример выхода 1 |
|
4 1 2 2 3 2 4 |
2 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
7 1 2 1 5 2 3 2 4 5 6 5 7 |
2 |
РЕШЕНИЕ
дерево
– динамическое программирование
Анализ алгоритма
Для каждой вершины v вычислим количество вершин sum[v]
в поддереве, где она
является корнем. Если to1, to2, …, tok – сыновья вершины v, то
sum[v] = 1 + sum[to1]
+ sum[to2] + … + sum[tok]
Если вершина v является листом дерева, то sum[v] = 1.
Пусть dp[v] равно количеству спасенных вершин в поддереве с корнем v, если на данный момент вершина v (и только она в поддереве) заражена.
Если вершина v имеет только одного сына to, то dp[v] = sum[to] – 1 (удаленная вершина to не является спасенной).
Пусть вершина v имеет двух сыновей to1 и to2 (каждая вершина имеет степень не
больше 3). Тогда у нас имеется два варианта:
·
Удалить to1 и рекурсивно спасать вершины
поддерева с корнем to2. Число спасенных вершин составит
sum[to1] – 1 + dp[to2].
·
Удалить to2 и рекурсивно спасать вершины
поддерева с корнем to1. Число спасенных вершин составит
sum[to2] – 1 + dp[to1].
Из двух
вариантов следует выбрать тот, при котором количество спасенных вершин будет
большим.
Рассмотрим
процесс поиска в глубину, когда рассматривается ребро (v, to).
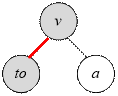
Пусть a – второй сын
вершины v. Нам следует
вычислить значение dp[to] + sum[a] – 1. Попробуем его найти, используя только вершины
v и to. Нам известно,
что
sum[v] = 1 + sum[to] + sum[a]
Откуда
sum[a] = sum[v] – sum[to] – 1
Следовательно
dp[to] + sum[a] – 1 = dp[to] + sum[v] – sum[to] – 2
Перебираем
сыновей to вершины v и вычисляем
dp[v] = max(dp[to] + sum[v] – sum[to] – 2)
Пример
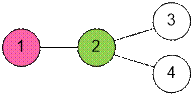
В
первом примере Хусейн сможет спасти две вершины 3 и 4, выбрав своим первым
ходом вершину номер 2.
Рассмотрим второй пример. Возле
каждой вершины v поставим метки sum[v] / dp[v]. Вершины, выбранные Хусейном,
отобразим зеленым цветом.
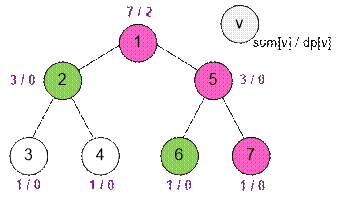
Например,
dp[1] = max(sum[2] – 1 + dp[5], sum[5] – 1 + dp[2]) =
max(2, 2) = 2,
sum[1] = 1 + sum[2] + sum[5] = 1 + 3 + 3 =
7
Реализация алгоритма
Объявим рабочие массивы.
#define MAX 300005
int sum[MAX], dp[MAX];
vector<vector<int>> g;
Функция dfs совершает поиск в глубину из вершины v. Предком вершины v является p.
void dfs(int v, int p = -1)
{
Инициализируем значения sum[v] и dp[v].
sum[v] = 1;
dp[v] = 0;
Запускаем поиск в глубину из сыновей вершины v.
for (int to : g[v])
if (to != p)
{
dfs(to, v);
sum[v] += sum[to];
}
Вычисляем значение dp[v].
for (int to : g[v])
if (to != p)
{
dp[v] = max(dp[v], sum[to] - 1); // if 1 son
dp[v] = max(dp[v], dp[to] + sum[v] - sum[to] - 2);
}
}
Основная часть программы. Читаем входные данные.
scanf("%d", &n);
g.clear();
g.resize(n + 1);
memset(dp,
0, sizeof(dp));
memset(sum,
0, sizeof(sum));
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
Запускаем поиск в глубину из вершины 1.
dfs(1);
Выводим ответ.
printf("%d\n", dp[1]);