11725. Два массива

Даны два числа n и m. Найдите количество таких пар массивов (a, b), что:

· оба массива имеют длину m;

· каждый элемент каждого массива – целое число от 1 до n включительно;

· a_i ≤ b_i для любого индекса i от 1 до m;

· массив a отсортирован в порядке неубывания;

· массив b отсортирован в порядке невозрастания.

Так как ответ может быть слишком большим, вычислите его по модулю 10⁹ + 7.

Вход. Два натуральных числа n и m (1 ≤ n ≤ 1000, 1 ≤ m ≤ 10).

Выход. Выведите одно число – количество массивов a и b, удовлетворяющих описанным выше условиям. Ответ выведите по модулю 10⁹ + 7.

Пример входа 1	Пример выхода 1
2 2	5
Пример входа 2	Пример выхода 2
723 9	157557417

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Рассмотрим объединённую последовательность:

a₁, a₂, …, a_m, b_m, b_m-1, …, b₁

Ее длина равна 2m. Из условия задачи следует, что эта последовательность:

· отсортирована в порядке неубывания;

· состоит из чисел от 1 до n.

Таким образом, задача сводится к подсчёту количества неубывающих последовательностей

1 ≤ x₁ ≤ x₂ ≤ … ≤ x_2m ≤ n

Выполним замену переменных:

y₁ = x₁ – 1,

y₂ = x₂ – x₁,

y₃ = x₃ – x₂,

…,

y_2m = x_2m – x_2m-1,

y_2m+1 = n – x_2m

Тогда все y_i ≥ 0, а их сумма равна

y₁ + y₂ + … + y_2m + y_2m+1 = n – 1

Следовательно, задача сводится к подсчёту количества способов разложить число n – 1 на 2m + 1 неотрицательных целых слагаемых. Каждому такому разложению соответствует ровно одна неубывающая последовательность x₁, x₂, …, x_2m, а значит – ровно одна пара массивов (a; b).

По классической формуле для сочетаний с повторениями число таких разложений равно (смотри задачу Еолимп 11551).

Пример

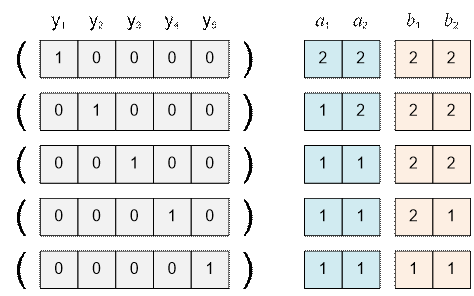
В первом тесте существуют 5 подходящих вариантов:

· a = [1, 1], b = [2, 2];

· a = [1, 2], b = [2, 2];

· a = [2, 2], b = [2, 2];

· a = [1, 1], b = [2, 1];

· a = [1, 1], b = [1, 1]

Соответствующая объединённая последовательность удовлетворяет неравенствам

1 ≤ a₁ ≤ a₂ ≤ b₂ ≤ b₁ ≤ 2

Сделаем замену переменных:

y₁ = a₁ – 1,

y₂ = a₂ – a₁,

y₃ = b₂ – a₂,

y₄ = b₁ – b₂,

y₅ = 2 – b₁

Просуммируем переменные:

y₁ + y₂ + … + y₅ = 1, y_i ≥ 0

Это уравнение имеет 5 решений. В каждом из них ровно одна переменная y_i равна 1, а все остальные равны 0. Рассмотрим соответствие этих решений исходным последовательностям:

Реализация алгоритма

Объявим константу и массив dp, для которого dp[n][k] = .

#define MOD 1000000007

long long dp[3001][30];

Функция Cnk вычисляет значение биномиального коэффициента .

long long Cnk(int n, int k)

{

if (n == k) return 1;

if (k == 0) return 1;

if (dp[n][k] != -1) return dp[n][k];

return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % MOD;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d", &n, &m);

Инициализируем массив dp.

memset(dp, -1, sizeof(dp));

Вычисляем и выводим ответ .

printf("%d\n", Cnk(n + 2 * m - 1, 2 * m));