11725. Two arrays

You are given two numbers n and m. Find the number of pairs of arrays (a, b) such that:

· both arrays have a length of m;

· each element of both arrays is an integer from 1 to n inclusive;

· a_i ≤ b_i for every index i from 1 to m;

· array a is sorted in non-decreasing order;

· array b is sorted in non-increasing order.

Since the result may be too large, compute it modulo 10⁹ + 7.

Input. Two positive integers n and m (1 ≤ n ≤ 1000, 1 ≤ m ≤ 10).

Output. Print a single number – the number of arrays a and b that satisfy the conditions described above. Print the result modulo 10⁹ + 7.

Sample input 1	Sample output 1
2 2	5
Sample input 2	Sample output 2
723 9	157557417

SOLUTION

combinatorics

Algorithm analysis

Consider the following sequence: a₁, a₂, …, a_m, b_m, b_m-1, …, b₁. Its length is 2m, it is sorted in non-decreasing order, and each of its elements lies within the interval from 1 to n. Let us compute the number of such sequences.

This sequence can be represented as:

1 ≤ x₁ ≤ x₂ ≤ … ≤ x_2m ≤ n

Now, let's perform a change of variables. Let:

y₁ = x₁ – 1, y₂ = x₂ – x₁, y₃ = x₃ – x₂, …, y_2m = x_2m – x_2m-1, y_2m+1 = n – x_2m

Now, each y_i ≥ 0, and the sum of these variables equals n – 1:

y₁ + y₂ + … + y_2m + y_2m+1 = n – 1

Now the task is to split the integer n – 1 into 2m + 1 terms, where each term can take non-negative integer values. Each such partition corresponds to one non-decreasing sequence x₁, x₂, …, x_2m.

The number of such partitions is equal to (see problem Eolymp 11551).

Example

In the first test, there are 5 suitable options:

· a = [1, 1], b = [2, 2];

· a = [1, 2], b = [2, 2];

· a = [2, 2], b = [2, 2];

· a = [1, 1], b = [2, 1];

· a = [1, 1], b = [1, 1]

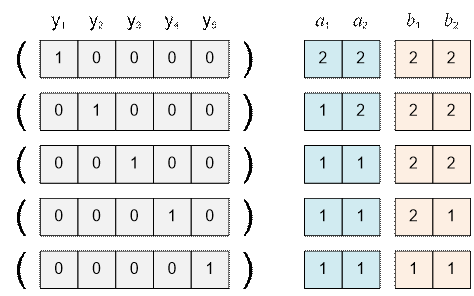
Consider the sequence: 1 ≤ a₁ ≤ a₂ ≤ b₂ ≤ b₁ ≤ 2.

Let’s perform a change of variables:

y₁ = a₁ – 1, y₂ = a₂ – a₁, y₃ = b₂ – a₂, y₄ = b₁ – b₂, y₅ = 2 – b₁

Summing the variables gives:

y₁ + y₂ + … + y₅ = 1, 0 ≤ y_i ≤ 1

This equation has 5 solutions. In each solution, one of the y_i values is 1, and the rest are 0. Let’s examine the correspondences between the solutions of the equation and the original sequences:

Algorithm realization

Declare a constant and an array dp, where dp[n][k] = .

#define MOD 1000000007

long long dp[3001][30];

The Cnk function computes the value of the binomial coefficient .

long long Cnk(int n, int k)

{

if (n == k) return 1;

if (k == 0) return 1;

if (dp[n][k] != -1) return dp[n][k];

return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % MOD;

}

The main part of the program. Read the input data.

scanf("%d %d", &n, &m);

Initialize the dp array.

memset(dp, -1, sizeof(dp));

Compute and print the answer .

printf("%d\n", Cnk(n + 2 * m - 1, 2 * m));