11726. Bernoulli scheme

There are n independent trials. The probability of event A occurring in each trial is p. Find the probability that in n independent trials, the random event A occurs exactly k times.

Input. The first line contains two integers n (0 < n ≤ 15) and k (0 ≤ k ≤ n).

The second line contains a real number p (0 ≤ p ≤ 1).

Output. Print the probability that in n independent trials, the random event A occurs exactly k times. The answer should be printed with a precision of at least 6 decimal places.

Sample input 1	Sample output 1
8 2 0.3	0.296475
Sample input 2	Sample output 2
10 3 0.5	0.117188

SOLUTION

probability

Algorithm analysis

A Bernoulli trial is an experiment with two possible outcomes:

· Success (the event occurs) with probability p,

· Failure (the event does not occur) with probability 1 – p.

A trial is called “Bernoulli” if it is independent and the probability of success remains constant throughout all trials.

The Bernoulli trial scheme is a series of independent trials, each of which is a Bernoulli trial. Let the number of trials be denoted by n. In each trial, the probability of success is p and the probability of failure is 1 – p, and these probabilities remain constant.

An example could be repeatedly flipping a coin. If we are interested in how many times heads will appear out of n flips, this would represent a Bernoulli trial scheme.

The number of successes in a series of n Bernoulli trials follows a binomial distribution. Let X be a random variable representing the number of successes in n trials. Then:

P(X = k) =

where

· p is the probability of success in each trial,

· k is the number of successes out of n trials.

To compute the value of the binomial coefficient with real numbers, we will use the following approach:

,

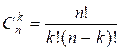It is known that ln n! = ln (1 * 2 * … * n) = ln 1 + ln 2 + … + ln n

Store the values of ln i! in the cells of an array lf[i]. Then we calculate

res = ln n! – ln k! – ln (n – k)! = lf[n] – lf[k] – lf[n – k],

After that

Example

In the first test, n = 8 trials are conducted. The probability of event A occurring in each trial is p = 0.3. We want to find the probability that event A occurs exactly k = 2 times. The desired probability is:

P(X = 2) = ≈ 0.296475

Algorithm realization

Declare an array lf, where lf[i] = ln i! = ln 1 + ln 2 + … + ln i.

#define MAX 1001

double lf[MAX];

Read the input data.

scanf("%d %d", &n, &k);

scanf("%lf", &p);

q = 1 - p;

Fill the array lf.

lf[1] = 0;

for (i = 2; i <= n; i++)

lf[i] = lf[i - 1] + log(i);

Compute the value of the binomial coefficient res = .

res = lf[n] - lf[k] - lf[n - k];

res = exp(res);

Compute the answer res = .

for (i = 0; i < k; i++)

res = res * p;

for (i = 0; i < n - k; i++)

res = res * q;

Print the answer.

printf("%lf\n", res);