1104. Домино
С домино можно
придумать множество развлечений. Например, дети любят выстраивать костяшки
домино в линию, располагая их рядом друг с другом. Если толкнуть одну костяшку,
она упадет и собьет соседнюю, та, в свою очередь, собьет следующую, и так
далее, пока цепная реакция не прекратится. Однако могут существовать такие
расстановки, при которых не все костяшки упадут. В этом случае необходимо
дополнительно толкнуть еще одну костяшку, чтобы цепная реакция продолжилась.
По заданной
расстановке домино определите минимальное количество костяшек, которые
необходимо толкнуть рукой, чтобы все домино упали.
Вход. Первая строка содержит два целых числа n и m (1 ≤ n, m ≤ 105), где n – количество костяшек
домино, а m – количество строк, описывающих их
взаимодействие. Костяшки пронумерованы числами от 1 до n.
Каждая из следующих m
строк содержит два числа x и y, которые означают, что если
костяшка с номером x упадет, то она собьет костяшку с номером y.
Выход. Выведите
одно число – минимальное количество костяшек,
которые нужно толкнуть, чтобы все домино упали.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 2 1 2 2 3 |
1 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 5 2 3 1 2 4 2 5 3 5 4 |
2 |
РЕШЕНИЕ
графы –
сильная связность
Анализ алгоритма
Рассмотрим задачу
нахождения сильных компонент связности в ориентированном графе. Каждую вершину
графа из одной
сильно связной
компоненты
окрасим в один и тот же цвет. Пусть color[i] обозначает цвет i-й вершины. Число
различных цветов окраски будет равно числу компонент сильной связности.
Очевидно, что если
толкнуть одну костяшку домино, то обязательно упадут все костяшки,
принадлежащие той же сильной компоненте связности. Обозначим через cnt количество сильных компонент связности.
Объявим массив used длины cnt, где used[i] = 1, если необходимо толкнуть домино из i-й
компоненты связности. Теперь определим, для каких значений used[i] следует
установить равным 0.
Переберем все
ребра графа. Нас интересуют только те ребра, которые соединяют разные
компоненты связности. Если такое ребро имеет вид i ® j (где color[i] ≠ color[j]), то установим used[color[j]]
= 0. Это означает, что нет необходимости толкать домино из компоненты цвета color[j], так как, толкнув домино из
компоненты цвета color[i], мы
гарантированно столкнем все домино из компоненты цвета color[j].
После обработки всех ребер
остается подсчитать количество единиц в массиве used. Это и будет
минимальное количество костяшек,
которые следует
толкнуть.
Пример
Графы,
приведенные в примерах, имеют следующий вид:
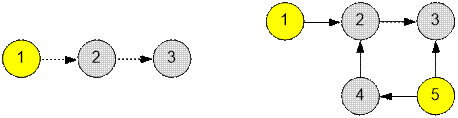
·
В первом примере достаточно столкнуть домино номер 1.
·
Во втором примере необходимо столкнуть домино с номерами 1
и 5.

Граф из первого
примера имеет
3 сильно
связные компоненты.
·
поскольку существует ребро (1, 2), нет необходимости толкать домино номер 2;
·
поскольку существует ребро (2, 3), нет необходимости толкать домино номер 3;
Реализация алгоритма
Входной граф
храним в списке смежности g.
Обратный граф
(граф, в котором изменены все направления ребер) храним списке смежности gr.
vector<vector<int> > g, gr;
vector<int>
used, top, color;
Функция dfs1 выполняет поиск в глубину на входном графе.
В массив top заносим вершины в
порядке завершения их обработки в процессе поиска в глубину.
void dfs1(int v)
{
used[v] = 1;
for (int to : g[v])
if
(!used[to]) dfs1(to);
top.push_back(v);
}
Функция dfs2 выполняет поиск в глубину на обратном
графе. Все вершины, которые посещаются в ходе рекурсивного вызова функции dfs2,
принадлежат одной компоненте сильной связности. Каждую из таких вершин
окрашиваем в цвет c.
void dfs2(int v, int c)
{
color[v] = c;
for (int to : gr[v])
if
(color[to] == -1) dfs2(to, c);
}
Основная часть программы. Читаем входные данные. Строим
обратный граф.
scanf("%d
%d",&n,&m);
g.resize(n+1);
gr.resize(n+1);
cnt = 0;
for(i = 0; i < m; i++)
{
scanf("%d %d",&a,&b);
g[a].push_back(b);
gr[b].push_back(a);
}
Запускаем поиск в глубину на входном графе. Порядок завершения
обработки вершин сохраняем в массиве top.
used.resize(n+1);
for(i = 1; i <= n; i++)
if (!used[i]) dfs1(i);
Затем выполняем поиск в глубину на обратном графе. Вершины обратного графа
обрабатываются в порядке, в котором они находятся в массиве top,
начиная с конца (справа налево). Вершины, принадлежащие одной компоненте
сильной связности, окрашиваются в один цвет. Текущий цвет раскраски содержится в переменной c.
Для удобства дальнейшей обработки обернем массив top, после чего
будем обрабатывать вершины в нем слева направо.
color.assign(n+1,-1);
reverse(top.begin(),
top.end());
c = 0;
for (int v : top)
if (color[v] == -1) dfs2(v, c++);
Переменная c
содержит количество компонент сильной связности.
used.assign(c,1);
for (i = 1; i <
g.size(); i++)
for (int to : g[i])
Перебираем все ребра графа (i, to). Проверяем, находятся ли вершины i и to
в разных сильно связных компонентах. Это так, если они окрашены в разные цвета. В таком случае, если
столкнуть любое домино из компоненты сильной связности, которой принадлежит
вершина i, то обязательно упадет и домино to. Это означает, что
нет смысла сталкивать домино цвета color[to]. Поэтому устанавливаем
used[color[to]] = 0.
if (color[i] !=
color[to]) used[color[to]] = 0;
В переменной c подсчитываем количество домино, которые следует столкнуть. Если для какого-либо
цвета i выполняется условие used[i] = 1, это означает, что
никакое домино цвета i не упадет, независимо от того, какое домино
другого цвета мы столкнем. В этом случае обязательно придется столкнуть хотя бы
одно домино цвета i.
c =
0;
for(i = 0; i < used.size(); i++)
if (used[i]) c++;
Выводим ответ.
printf("%d\n",c);
Java реализация
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g, gr;
static int used[], color[];
static Vector<Integer> top = new Vector<Integer>();
static void dfs1(int v)
{
used[v] = 1;
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == 0) dfs1(to);
}
top.add(v);
}
static void dfs2(int v, int c)
{
color[v] = c;
for(int i = 0; i < gr[v].size(); i++)
{
int to = gr[v].get(i);
if (color[to] == -1) dfs2(to,c);
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
gr = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
gr[i] = new ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
gr[b].add(a);
}
used = new int[n+1];
for(int i = 1; i <= n; i++)
if (used[i] == 0) dfs1(i);
color = new int[n+1];
Arrays.fill(color, -1);
int c = 0;
for(int i = 1; i <= n; i++)
{
int v = top.get(n-i);
if (color[v] == -1) dfs2(v,c++);
}
used = new int[c];
Arrays.fill(used, 1);
for(int i = 1; i < g.length; i++)
for(int j = 0; j < g[i].size(); j++)
{
int to = g[i].get(j);
// check edge i -> j if they in
the same scc.
if (color[i] != color[to]) used[color[to]] = 0;
}
c = 0;
for(int i = 0; i < used.length; i++)
if (used[i] == 1) c++;
System.out.println(c);
con.close();
}
}