1104. Dominos
Dominoes can inspire a variety of entertaining activities.
For example, children enjoy arranging domino tiles in a line, placing them side
by side. If you push one tile, it falls and knocks down the next one, which in
turn knocks down the following one, and so on, until the chain reaction stops.
However, there might be setups where not all tiles fall. In such cases, you
need to push an additional tile to keep the chain reaction going.
Given a specific arrangement of dominoes, determine the
minimum number of tiles that need to be pushed by hand to make all the dominoes
fall.
Input. The first line contains two
integers n and m (1 ≤ n, m ≤ 105), where n is the number of domino tiles, and m
is the number of lines describing their interactions. The dominoes are numbered
from 1 to n.
Each of the following m lines contains two integers x
and y, indicating that if the domino numbered x falls, it will
knock over the domino numbered y.
Output. Print one integer – the minimum number of domino tiles that need to be pushed to
make all the dominoes fall.
|
Sample
input 1 |
Sample
output 1 |
|
3 2 1 2 2 3 |
1 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
5 5 2 3 1 2 4 2 5 3 5 4 |
2 |
SOLUTION
graphs – strong
connected components
Algorithm analysis
Let us consider the
problem of finding strongly connected components in a directed graph. Each
vertex in one strongly connected component will be assigned the same color. Let
color[i] denote the color of the i-th vertex. The number of
distinct colors will equal the number of strongly connected components.
It is obvious that if one
domino tile is pushed, all tiles belonging to the same strongly connected
component will inevitably fall. Let cnt
represent the number of strongly connected components.
We’ll define an
array used of length cnt, where used[i] = 1 if it is necessary to push a domino in
the i-th component. Now, let us determine for which values of used[i]
we should set it to 0.
Iterate through
all edges of the graph. We are interested only in the edges that connect
different strongly connected components. If such an edge is of the form i ® j (where color[i] ≠
color[j]), then set used[color[j]] = 0. This means there is no need to
push a domino from the component with color color[j], because by pushing a domino from the component with color color[i], we’ll guaranteedly topple all dominoes in
the component with color color[j].
After processing
all edges, count the number of ones in the array used. This will be
the minimum number of domino tiles that need to be pushed.
Example
The graphs from the
examples have the following form:
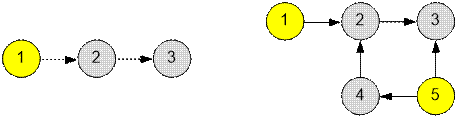
·
In the first example, it is enough to push domino number 1.
·
In the second example, it is necessary to push dominoes
numbered 1 and 5.

The graph in the first
example has 3 strongly connected components.
·
Since there is an edge (1, 2), there is no need to push
domino number 2;
·
Since there is an edge (2, 3), there is no need to push
domino number 3;
Algorithm implementation
The input graph is stored in
the adjacency list g.
The reverse graph (a graph
where all edge directions are reversed) is stored in the adjacency list gr.
vector<vector<int> > g, gr;
vector<int>
used, top, color;
The
function dfs1
performs a depth-first search on the input graph. Vertices are added to the
array top in the order of their processing completion during the dfs.
void dfs1(int v)
{
used[v] = 1;
for (int to :
g[v])
if
(!used[to]) dfs1(to);
top.push_back(v);
}
The
function dfs2 performs a depth-first search on the reverse graph. All vertices
visited during a recursive call of dfs2 belong to the same
strongly connected component. Each of these vertices is assigned the color c.
void dfs2(int v, int c)
{
color[v] = c;
for (int to :
gr[v])
if
(color[to] == -1) dfs2(to, c);
}
The main part of the program. Read the input data. Construct the reverse
graph.
scanf("%d
%d",&n,&m);
g.resize(n+1);
gr.resize(n+1);
cnt = 0;
for(i = 0; i < m; i++)
{
scanf("%d %d",&a,&b);
g[a].push_back(b);
gr[b].push_back(a);
}
Prform a depth-first search on the input graph, storing the order in which
vertices finish processing in the array top.
used.resize(n+1);
for(i = 1; i <= n; i++)
if (!used[i]) dfs1(i);
Next, perform a depth-first search on the reverse graph. The
vertices of the reverse graph are processed in the order they appear in the
array top, starting from the end (right to left). Vertices belonging to
the same strongly connected component are assigned the same color. The current
color used for coloring is stored in the variable c.
For convenience in further processing, we reverse the array top,
allowing us to process its vertices from left to right.
color.assign(n+1,-1);
reverse(top.begin(),
top.end());
c = 0;
for (int v : top)
if (color[v] == -1) dfs2(v, c++);
The variable c contains the number of strongly connected
components.
used.assign(c,1);
for (i = 1; i <
g.size(); i++)
for (int to : g[i])
Iterate through all edges of the graph (i,
to). Check whether the vertices i
and to belong to different strongly connected components. This is true
if they are colored with different colors. In such a case, if we push any
domino from the strongly connected component to which vertex i belongs,
domino to will inevitably fall as well. This means there is no need to
push a domino of color color[to]. Therefore, set used[color[to]]
= 0.
if (color[i] !=
color[to]) used[color[to]] = 0;
The variable c keeps track of the number of dominoes that need to
be pushed. If for any color i, the condition used[i] = 1 holds,
it means that no domino of color i will fall regardless of which domino
of another color is pushed. In this case, it will be necessary to push at least
one domino of color i.
c =
0;
for(i = 0; i < used.size(); i++)
if (used[i]) c++;
Print the answer.
printf("%d\n",c);
Java implementation
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g, gr;
static int used[], color[];
static Vector<Integer> top = new Vector<Integer>();
static void dfs1(int v)
{
used[v] = 1;
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == 0) dfs1(to);
}
top.add(v);
}
static void dfs2(int v, int c)
{
color[v] = c;
for(int i = 0; i < gr[v].size(); i++)
{
int to = gr[v].get(i);
if (color[to] == -1) dfs2(to,c);
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
gr = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
gr[i] = new ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
gr[b].add(a);
}
used = new int[n+1];
for(int i = 1; i <= n; i++)
if (used[i] == 0) dfs1(i);
color = new int[n+1];
Arrays.fill(color, -1);
int c = 0;
for(int i = 1; i <= n; i++)
{
int v = top.get(n-i);
if (color[v] == -1) dfs2(v,c++);
}
used = new int[c];
Arrays.fill(used, 1);
for(int i = 1; i < g.length; i++)
for(int j = 0; j < g[i].size(); j++)
{
int to = g[i].get(j);
// check edge i -> j if they in the same scc.
if (color[i] != color[to]) used[color[to]] = 0;
}
c = 0;
for(int i = 0; i < used.length; i++)
if (used[i] == 1) c++;
System.out.println(c);
con.close();
}
}