1105. Hello, Pie!
Pizzeria Pizazz prides
itself on delivering pizza to its customers as fast as possible. Unfortunately,
only one driver can be hired for delivery. Before delivery, he waits until a
certain number of orders arrive (from 1 to 20). The driver
prefers to choose the fastest route for delivering all orders, even if he has
to pass the same place several times, including a pizzeria. At the end of the
delivery, the driver must return to the original place, that is, to the
pizzeria. You need to write a program that finds such a route.
Input.
The first line contains the number of orders n (1 ≤ n ≤ 20).
This is followed by n + 1 strings,
each containing n + 1 integers.
These numbers indicate the travel time between the pizzeria (its number is 0)
and n places where orders are located
(they are numbered from 1 to n).
The j - th value of the i - th line indicates the time it
takes to drive directly from the location i
to the location j, without visiting
any other places along the way. Note that travel between i and j may not be faster
directly, but through other locations due to traffic jams and traffic lights.
Travel times are not symmetrical. That is, the time it takes to drive directly
from i to j does not always coincide with the travel time directly from j to i.
Output. Print one number – the shortest time it takes to deliver pizza to all
customers and return back to pizzeria.
|
Sample input |
Sample output |
|
3 0 1
10 10 1 0 1
2 10 1
0 10 10 2
10 0 |
8 |
SOLUTION
graphs – travelling
salesman problem
Algorithm analysis
Using the Floyd-Worshall algorithm,
construct a matrix m in which m[i][j] contains the
shortest time it takes to get from i
to j.
Then, using the matrix m,
by exhaustive search (using backtracking), find the Hamiltonian cycle of the
least weight. This solution will give Time
Limit.
To run the code in time, one should implement the dynamic
programming using masks as in the traveling salesman problem.
Example
The input graph is shown on the left. The shortest distance graph is given on the right.
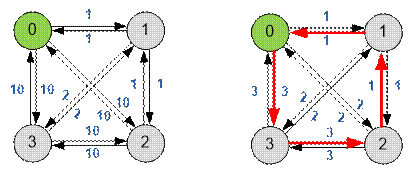
The optimal
path is 0 → 1 → 3 → 1
→ 2 → 1 → 0 of length 8.
Algorithm realization
Define the variable INF that equals to infinity, the maximum
possible number of vertices in the graph MAX, and an array dp, where we’ll store the dynamically recomputed values dp(S, i).
Each subset S will be stored as a number, in which the i -
th bit is equal to 1 if the vertex with the number i is
present in it, and zero otherwise. For example, for n = 5, the
subset {1, 4, 5} is encoded with 110012 = 25.
#define MAX 22
#define INF 0x3F3F3F3F
int dp[1<<MAX][MAX+1];
The travel time
between points store in the array m.
int m[MAX][MAX];
Function solve computes the value dp(S, last),
where the set S is encoded by the integer mask. Moreover, S \ {last}
equals to mask ^
(1<< last). Next, iterate over all i, i Î S \ {last} and look for the minimum value res among
dp(S \ {last}, i) + m[i][last]. The
variable res points to the cell dp[mask][last],
so when res changes, the value of dp[mask][last]
also changes.
int solve(int mask, int last)
{
int &res =
dp[mask][last];
if(res ==
INF)
{
mask ^= (1 << last);
for(int i = 1; i < n + 1; ++i)
if(mask
& (1 << i)) res = min(res,solve(mask,i) + m[i][last]);
}
return res;
}
The main
part of the program. Read
the input data.
scanf("%d",&n);
for(i = 0; i < n + 1; i++)
for(j = 0; j < n + 1; j++)
scanf("%d",&m[i][j]);
Using the Floyd – Worshall algorithm, compute the shortest travel
time between all pairs of places.
for(k = 0; k < n + 1; k++)
for(i = 0; i < n + 1; i++)
for(j = 0; j < n + 1; j++)
if (m[i][k] + m[k][j] < m[i][j]) m[i][j] = m[i][k]
+ m[k][j];
Initially, the values of dp(S, i) are
unknown, set them equal to plus infinity. The set {0} corresponds to the mask
1, set dp({0}, 0) =
0 (the minimum path from the zero vertex to it without visiting other vertices
is equal to zero). Store the
required minimum cycle length in the variable best.
memset(dp,0x3F,sizeof(dp));
dp[1][0] = 0; best = INF;
Set dp({0, i}, i)
= m[0][i] (vertex 0 is the location of pizzeria).
for(i = 1; i < n + 1; i++) dp[1 | (1 << i)][i] =
m[0][i];
Compute the
Hamiltonian cycle of minimum length. The value 2n+1 – 1 corresponds
to the set {0, 1, 2, ..., n}. Compute the minimum among all values
of dp({0, 1, 2, ..., n}, i) + m[i][0],
1 £ i £ n.
for(i = 1; i < n + 1; i++)
best = min(best, solve((1 << (n + 1)) -
1,i) + m[i][0]);
Print the required
minimum cycle length.
printf("%d\n",best);