1106. Танцы на вечеринке
На вечеринку
приглашены n мальчиков и n девочек. Они хотят станцевать
несколько раундов.
В каждом раунде
гости делятся на n танцующих пар.
Каждый гость должен быть в некоторой паре, каждая пара должна состоять из
одного мальчика и одной девочки. В каждом раунде каждый мальчик должен
танцевать с другой девочкой. Некоторые мальчики и девочки не нравятся друг
другу. Каждый мальчик может танцевать не более чем с k девочками, которые ему не нравятся. Аналогично каждая девочка
может танцевать не более чем с k
мальчиками, которые ей не нравятся.
Имеется
информация о том, нравятся ли друг другу i-ый
мальчик и j-ая девочка (1 ≤ i, j
≤ n). Найти наибольшее
количество раундов, которое можно станцевать на вечеринке.
Вход. Первая строка содержит два числа: n и k (1 ≤ n ≤ 50, 0 ≤ k ≤ 50). j-ый
символ в i-ой строке матрицы содержит
‘Y’, если i-ый мальчик и j-ая девочка нравятся друг другу, и 'N' в
противном случае.
Выход. Вывести наибольшее количество раундов,
которое можно станцевать на вечеринке.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 0 YYY YYN YNY |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
2 1 YN YN |
1 |
РЕШЕНИЕ
графы -
паросочетания
Анализ алгоритма
Рассмотрим
следующую задачу: могут ли танцы продолжаться в точности m раундов? Если мы сможем ответить на этот вопрос, то бинарным
поиском найдем наибольшее m, для
которого проведение танцев возможно.
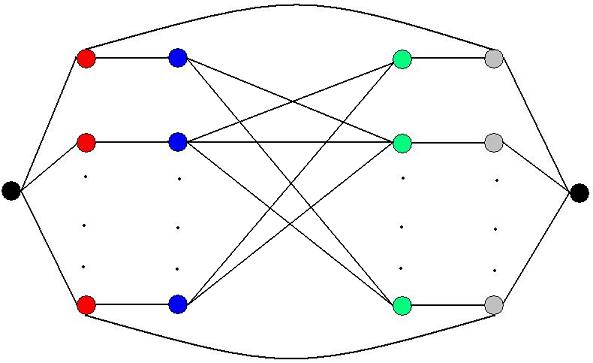
Построим граф, имеющий один исток и один сток
(черные вершины). Красные вершины представляют мальчиков, серые – девочек. Если
мальчик и девочка нравятся друг другу, то проведем между ними ребро единичной
пропускной способности (на рисунке такими являются два ребра – верхнее и
нижнее). Иначе добавим синие и зеленые вершины как показано на рисунке и
установим пропускную способность ребер между соответствующими синими и зелеными
вершинами равную 1.
Синие и зеленые
вершины образуют “защитный” уровень. Связь мальчиков с девочками, которые друг
другу не нравятся, будет проходить по ребрам защитного уровня. Каждый мальчик
может танцевать не более чем с k
девочками, которые ему не нравятся. Установим пропускную способность ребер
между красными и синими, зелеными и серыми вершинами равную k. Таким образом, между каждым мальчиком
и каждой девочкой будет установлена связь через ребро либо напрямую, либо через
вершины защитного уровня.
Танцы должны
продолжаться в точности m раундов.
Установим пропускную способность ребер между истоком и красными вершинами, а
также между серыми вершинами и стоком равную m.
Находим
максимальный поток в графе. Танцы могут продолжаться в точности m раундов тогда и только тогда, когда
величина максимального потока будет равна n
* m, где n – количество мальчиков.
При построении
матрицы пропускных способностей g вершины графа имеют следующие номера:
·
исток: номер 0;
·
красные вершины: от 1 до n;
·
синие вершины: от n
+ 1 до 2*n;
·
зеленые вершины: от 2*n
+ 1 до 3*n;
·
серые вершины: от 3*n
+ 1 до 4*n;
·
сток: номер 4*n
+ 1;
Реализация алгоритма
Объявим матрицу
пропускных способностей g и массива used. Входную матрицу отношений между
мальчиками и девочками храним в массиве строк likes.
#define MAX 52
int g[4*MAX][4*MAX], used[4*MAX];
vector<string> likes;
Вычисление потока на дополняющем пути,
ведущего из вершины x в t.
int aug(int x,int t,int CurFlow)
{
if (x == t) return
CurFlow;
if (used[x]++) return
0;
for (int Flow, y = 0;
y <= 4 * n + 1; y++)
{
if (g[x][y] > 0 && (Flow =
aug(y,t,min(CurFlow,g[x][y]))))
{
g[x][y] -= Flow; g[y][x] += Flow;
return Flow;
}
}
return 0;
}
Функция CanDance возвращает 1, если дети смогут танцевать m раундов.
int CanDance(int m)
{
int i, j;
for(i = 1; i <= n; i++) g[0][i] = g[3*n+i][4*n+1]
= m;
for(i = 1; i <= n; i++) g[i][n+i] =
g[2*n+i][3*n+i] = k;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
if (likes[i][j] == 'Y') g[i+1][3*n+j+1] = 1;
else g[n+i+1][2*n+j+1] = 1;
MaxFlow = 0;
do
{
memset(used,0,sizeof(used));
} while ((flow =
aug(0,4*n+1,0x7FFFFFFF)) && (MaxFlow += flow));
return MaxFlow == m*n;
}
Используя бинарный поиск, функция maxDances возвращает
максимальное количество раундов, которое смогут танцевать мальчики и девочки.
int maxDances(void)
{
int m, low = 0, high = n;
while(low < high)
{
m = (low + high + 1) / 2;
if(CanDance(m)) low = m; else high = m - 1;
}
return low;
}
Основная часть программы. Читаем входную
матрицу отношений между мальчиками и девочками в массив строк likes.
scanf("%d
%d\n",&n,&k);
memset(g,0,sizeof(g));
likes.clear();
for(i = 0; i < n; i++)
{
gets(line);
likes.push_back(line);
}
Вычисляем максимальное количество раундов, которое смогут
танцевать дети, и выводим его.
res = maxDances();
printf("%d\n",res);