1108

1108. Червячные дыры

В 2163 году были обнаружены червячные дыры. Червячная дыра представляет собой тоннель сквозь пространство и время, соединяющий две звездные системы. Эти дыры имеют следующие свойства:

· Червячные дыры являются односторонними.

· Время путешествия по любому тоннелю равно нулю.

· Червячная дыра имеет два конца, каждый из которых находится в звездной системе.

· Звездная система в своих границах может иметь несколько концов червячных дыр.

По некоторой неизвестной причине начиная с нашей Солнечной системы всегда можно достигнуть любую другу звездную систему перемещаясь некоторой последовательностью червячных дыр (возможно, это потому что Земля является центом универсума).

Между любой парой звездных систем существует не более одной червячной дыры в любом из направлений.

Оба конца червячной дыры не могут находиться в одной звездной системе.

Каждая червячная дыра перемещает путешественника на определенное константное количество лет вперед или назад. Например, одна дыра может переместить на 15 лет в будущее, а другая на 42 лет в прошлое.

Известный физик, живущий на Земле, хочет использовать червячные дыры для исследования теории Большого Взрыва. Поскольку двигатель искривления пространства еще не изобретен, невозможно напрямую путешествовать между звездными системами. Однако это можно делать при помощи червячных дыр.

Ученый хочет достигнуть цикла червячных дыр, который поможет ей попасть в прошлое. Двигаясь по этому циклу несколько раз, можно прийти ко времени, когда имел место Большой Взрыв и наблюдать его собственными глазами. Напишите программу, которая определяет существование такого цикла.

Вход. Первая строка содержит количество звездных систем n (1 ≤ n ≤ 1000) и количество червячных дыр m (0 ≤ m ≤ 2000). Звездные системы пронумерованы от 0 (наша солнечная система) до n – 1. Каждая червячная дыра описывается в отдельной строке и содержит три целых числа x, y и t. Эти числа указывают на возможность передвижения из звездной системы с номером x в звездную систему с номером y, при этом время изменяется на t (-1000 ≤ t ≤ 1000) лет.

Выход. Строка содержит информацию, возможно ли в заданном множестве систем попасть в минус бесконечность во времени, используя червячные дыры. Выводить следует строку “possible” или “not possible”.

Пример входа 1	Пример выхода 1
3 3 0 1 1000 1 2 15 2 1 -42	possible

Пример входа 2	Пример выхода 2
4 4 0 1 10 1 2 20 2 3 30 3 0 -60	not possible

РЕШЕНИЕ

графы – алгоритм Беллмана-Форда

Анализ алгоритма

Если в графе существует цикл отрицательной длины, то двигаясь по нем можно попасть в бесконечное прошлое. Для проверки существования такого цикла следует воспользоваться алгоритмом Беллмана – Форда.

Обозначим через d[v] верхнюю оценку веса кратчайшего пути из начальной вершины s в вершину v. Пусть w(u, v) – вес ребра (u, v). Релаксацией ребра (u, v) называется уменьшение значения d[v] до d[u] + w(u, v) (если второе значение меньше первого).

Relax(u, v, w)

if (d[v] > d[u] + w(u, v)) then d[v] = d[u] + w(u, v);

Изначально следует положить значения d[v] для всех v Î V(G) \ {s} равными плюс бесконечности, а d[s] = 0. Это совершается в процедуре инициализации.

инициализация (G, s)

for всех вершин v Î V(G) do d[v] = ¥;

d[s] = 0;

Функция Bellman_Ford совершает релаксацию всех ребер |V(G)| – 1 раз. Если в графе присутствует цикл отрицательной длины, то по завершению предыдущей операции существует ребро (u, v), для которого выполняется неравенство d[v] > d[u] + w(u, v). Функция Bellman_Ford возвращает FALSE, если найден цикл отрицательной длины и TRUE иначе.

Bellman_Ford(G, w, s)

иницализация (G, s)

for i = 1 to |V(G)| – 1 do

for каждого ребра (u, v) Î E(G) do Relax(u, v, w);

for каждого ребра (u, v) Î E(G) do

if d[v] > d[u] + w(u, v) then return FALSE;

return TRUE;

Поскольку землянин стартует с Солнечной системы, то начальной будет вершина с номером 0, то есть s = 0.

Лемма. Пусть d(s, v) – длина кратчайшего пути от s до v. Пусть G(V, E) – взвешенный ориентированный граф с весовой функцией w, не содержащий циклов отрицательного веса, достижимых из s. Тогда по окончании работы процедуры Bellman_Ford будет выполняться равенство d[v] = d(s, v) для всех вершин v, достижимых из s.

Лемма. Если в графе существует цикл отрицательной длины, то существует ребро (u, v), для которого выполняется неравенство d[v] > d[u] + w(u, v).

Доказательство. Пусть (v₀, v₁, …, v_k = v₀) – цикл отрицательной длины, достижимый из исходной вершины, но при этом d[v_i₊₁] £ d[v_i] + w(v_i, v_i₊₁) для всех i = 0, 1, …, k – 1. Сложив эти k неравенств, и сократив на , получим: 0 £ . Последнее неравенство противоречит тому что (v₀, v₁, …, v_k = v₀) является циклом отрицательной длины. Сокращаемая сумма конечна, так как все вершины v_i достижимы.

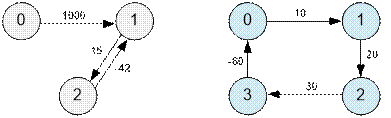
Пример

Графы из примеров имеют следующий вид.

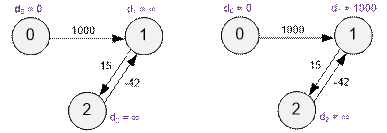
Рассмотрим первый пример. Слева показано начальное состояние графа. Справа – состояние графа после первой релаксации всех ребер.

Второй раз совершим релаксацию всех ребер:

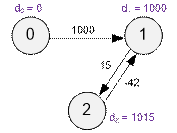
Для ребра (2, 1) имеет место неравенство: d[1] > d[2] + w(2, 1) (1000 > 1015 – 42). Значит существует цикл отрицательной длины, в который входит ребро (2, 1). Таким циклом будет 1 – 2 – 1 и его величина равна 15 – 42 = -27.

Во втором тесте циклов отрицательной длины нет.

Реализация алгоритма

Информацию о червячных дырах храним в массивах x, y и w. i-ая червячная дыра начинается в звездной системе с номером x[i] и ведет в звездную систему с номером y[i], при этом время изменяется на w[i] лет. Массив d хранит верхнюю оценку веса кратчайшего пути из начальной до остальных вершин.

#define MAX 2001

int x[MAX], y[MAX], w[MAX], d[MAX];

Реализация алгоритма Беллмана – Форда.

int Bellman_Ford(void)

{

int i, j;

Стартовой вершиной объявляем нулевую (нашу солнечную систему).

memset(d,0x3F,sizeof(d));

d[0] = 0;

Совершаем релаксацию всех ребер |V(G)| – 1 раз.

for(i = 0; i < n; i++)

Проходим по всем m ребрам и релаксируем их. Ребро (u, v) релаксируем, если значение d[u] не равно плюс бесконечности.

for (j = 0; j < m; j++)

if (d[x[j]] < 0x3F3F3F3F)

if (d[y[j]] > d[x[j]] + w[j])

d[y[j]] = d[x[j]] + w[j];

Проверяем, существует ли ребро, которое релаксирует. Если да – то в графе существует цикл отрицательной длины. Иначе такого цикла не существует.

for(j = 0; j < m; j++)

if (d[y[j]] > d[x[j]] + w[j]) return 0;

return 1;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&n,&m);

for(i = 0; i < m; i++)

scanf("%d %d %d",&x[i],&y[i],&w[i]);

Запускаем алгоритм Беллмана – Форда и выводим ответ.

if (Bellman_Ford()) printf("not ");

printf("possible\n");