1109. 106 миль до Чикаго
В фильме “Братья
Блюз” детский дом, в котором воспитывались Элвуд и Джек, должен быть
продан Совету по Образованию, если они
только не уплатят 5000 долларов налогов в офисе Кука в Чикаго. Сыграв концерт в
Палас Отеле и заработав 5000 долларов, им надо найти дорогу в Чикаго. Но это не
так просто как кажется, так как за ними гонится полиция, местная банда и группа
нацистов. Более того, до Чикаго
Поскольку у них
миссия от Бога, Вы должны помочь найти им самый безопасный путь в Чикаго. Самым
безопасным считается путь, на котором вероятность быть не пойманными
максимальна.
Вход. Первая строка
содержит два числа n и m (2 ≤ n ≤ 100 , 1 ≤ m
≤ n * (n – 1) / 2). n –
количество перекрестков, m – количество
улиц.
Следующие m строк описывают улицы. Каждая улица
описывается тремя целыми числами a, b и p
(1 ≤ a, b ≤ n , a ≠ b, 1 ≤ p ≤
100): a и b – концы улицы, а p –
вероятность в процентах того что Братья Блюз пройдут по улице незамеченными. Все
улицы двусторонние. Между любыми двумя перекрестками существует не более одной
улицы.
Выход. Вычислить
вероятность выбора безопасной дороги от перекрестка 1 (Палас Отель) до
перекрестка n (плаза Дж. Дейли в
Чикаго). Считайте, что хотя бы один такой путь обязательно существует между
перекрестками 1 и n.
Искомую
вероятность следует вывести в процентах с 6 знаками после десятичной запятой. Результат
следует выводить в формате, приведенном ниже.
|
Пример входа |
Пример выхода |
|
5 7 5 2
100 3 5
80 2 3
70 2 1
50 3 4
90 4 1
85 3 1
70 |
61.200000
percent |
РЕШЕНИЕ
графы – алгоритм Дейкстры
Анализ алгоритма
Задача решается алгоритмом Дейкстры. Только в операции
релаксации используется не суммирование длин дорог, а произведение вероятностей
быть не пойманными. Значение d[i]
соответствует не кратчайшему пути до вершины i, а максимальной вероятности быть не пойманными на пути из
начальной вершины до вершины i.
Пусть:
·
p1 (0 ≤ p1 ≤ 1) –
вероятность быть не пойманным на пути из A в B;
·
p2 (0 ≤ p2 ≤
1) – вероятность быть не пойманным на пути из B в C;
Тогда
вероятность быть не пойманным на пути из A в C равна p1 * p2.
![]()
Пример
Рассмотрим граф,
заданный в примере.
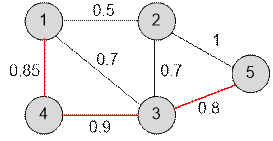
Наиболее
безопасным путем будет 1 ® 4 ® 3 ® 5. Вероятность быть не пойманным на нем равна 0.85 * 0.9
* 0.8 = 0.612.
Например:
·
на пути 1 ® 3 ® 5 ответ будет
0.7 * 0.8 = 0.56.
·
на пути 1 ® 2 ® 5 ответ будет
0.5 * 1 = 0.5.
·
на пути 1 ® 3 ® 2 ® 5 ответ будет
0.7 * 0.7 * 1 = 0.49.
Реализация алгоритма
Объявим массивы,
используемые в алгоритме Дейкстры. Матрица расстояний хранится в массиве mas.
int used[MAX];
double mas[MAX][MAX], d[MAX];
Читаем входные
данные. Делим значения вероятностей на 100 так чтобы их значения лежали в
промежутке от 0 до 1.
scanf("%d %d",&n,&m);
memset(mas,0,sizeof(mas));
while(m--)
{
scanf("%d %d
%d",&i,&j,&per);
mas[i][j] = mas[j][i] = per / 100.0;
}
Запускаем алгоритм Дейкстры. Исток находится в первой
вершине (Палас Отель).
memset(used,0,sizeof(used));
memset(d,0,sizeof(d)); d[1] = 1;
for(i = 1; i < n; i++)
{
max = 0;
for(j = 1; j
<= n; j++)
if
(!used[j] && d[j] > max) {max = d[j]; w = j;}
for(j = 1; j
<= n; j++)
if (!used[j]) d[j] = maximum(d[j],d[w] * mas[w][j]);
used[w] = 1;
}
Выводим вероятность выбора безопасной дороги в процентах,
ведущей в n-ую вершину графа (плаза
Дж. Дейли в Чикаго).
printf("%.6lf percent\n",d[n]*100);