1109. 106 miles to Chicago
In the movie “Blues Brothers”,
the orphanage where Elwood and Jack were raised may be sold to the Board of
Education if they do not pay 5000 dollars in taxes at the Cook Country Assessor’s
Office in Chicago. After playing a gig in the Palace Hotel ballroom to earn
these 5000 dollars, they have to find a way to Chicago. However, this is not so
easy as it sounds, since they are chased by the Police, a country band and a
group of Nazis. Moreover, it is 106 miles to Chicago, it is dark and they are
wearing sunglasses.
As they are on a mission
from God, you should help them find the safest way to Chicago. In this problem,
the safest way is considered to be the route which maximizes the probability
that they are not caught.
Input.
The first line contains two integers n
and m (2
≤ n ≤ 100 , 1 ≤ m ≤ n * (n – 1) / 2), where n is the number of intersections, m is the number of
streets to be considered.
The next m lines contain the description of the
streets. Each street is described by a line containing 3 integers a, b
and p (1
≤ a, b ≤ n , a ≠ b, 1 ≤ p ≤
100): a and b are the two end points of the street and p is the probability in percent that the Blues Brothers will manage
to use this street without being caught. Each street can be used in both
directions. You may assume that there is at most one street between two end
points.
Output. Calculate the probability of the safest path from intersection 1 (the
Palace Hotel) to intersection n (the
Honorable Richard J. Daley Plaza in Chicago). You can assume that there is at
least one path between intersection 1 and n.
Print the probability as a
percentage with exactly 6 digits after the decimal point. Adhere to the format
shown below.
|
Sample input |
Sample output |
|
5 7 5 2
100 3 5
80 2 3
70 2 1
50 3 4
90 4 1
85 3 1
70 |
61.200000
percent |
SOLUTION
graphs – Dijkstra’s
algorithm
Algorithm analysis
The problem is solved by Dijkstra’s algorithm. Only in the relaxation we do not
sum up the lengths of the roads, but compute the product of the probabilities of not being caught. The
value d[i] does not correspond to the
shortest path to vertex i, but to the maximum
probability of not being caught on the way from the initial vertex to the vertex i.
Suppose:
·
p1 (0 ≤ p1 ≤ 1) be the probability of not being caught on the way from A to B;
·
p2 (0 ≤ p2 ≤
1) be the probability of not being caught on the way from B to C;
Then the
probability of not being caught on the way from A to C is p1 * p2.
![]()
Example
Consider the graph given in a sample.
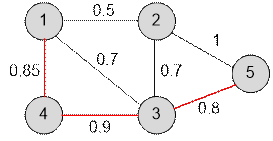
The safest path will be 1 ® 4 ® 3 ® 5. The probability of not being caught on it is 0.85 * 0.9 * 0.8
= 0.612.
For example:
·
on
the path 1 ® 3 ® 5 the
answer is 0.7 * 0.8 = 0.56.
·
on
the path 1 ® 2 ® 5 the
answer is 0.5 * 1 = 0.5.
·
on
the path 1 ® 3 ® 2 ® 5 the
answer is 0.7 * 0.7 * 1 = 0.49.
Algorithm realization
Declare the
arrays used in Dijkstra’s
algorithm. The distance matrix is stored in the array mas.
int used[MAX];
double mas[MAX][MAX], d[MAX];
Read the input
data. Divide the probabilities by 100 so that their values will be in the range from 0 to 1.
scanf("%d %d",&n,&m);
memset(mas,0,sizeof(mas));
while(m--)
{
scanf("%d %d
%d",&i,&j,&per);
mas[i][j] = mas[j][i] = per / 100.0;
}
Start the Dijkstra’s algorithm. The
source is located at the
first vertex (Palace
Hotel).
memset(used,0,sizeof(used));
memset(d,0,sizeof(d)); d[1] = 1;
for(i = 1; i < n; i++)
{
max = 0;
for(j = 1; j
<= n; j++)
if
(!used[j] && d[j] > max) {max = d[j]; w = j;}
for(j = 1; j
<= n; j++)
if (!used[j]) d[j] = maximum(d[j],d[w] * mas[w][j]);
used[w] = 1;
}
Print
the probability of choosing the safest road in percent, leading to the n-th vertex of the graph (J. Daley Plaza in Chicago).
printf("%.6lf percent\n",d[n]*100);