1110. Гнездо орла
“Гнездо орла” представляет
собой приключенческую игру. Основной смысл игры состоит в уничтожении хороших
парней, создании общественного порядка, сборе денег с незаконной деятельности,
постепенно превращаясь в успешного гангстера. Но быть гангстером не так просто
в этой игре.
Игра имеет
нелинейную сюжетную линию, которая позволяет игроку выбирать одну из нескольких
альтернативных миссий. Однако здесь есть одна ловушка. Игрок каждый раз может
выбирать миссии, сложность которых больше чем любая из предыдущих законченных. И
когда миссия закончена, она больше не доступна игроку. Единственное исключение
составляют первая и последняя миссии, которые никогда не удаляются и даже не
представлены в списке возможных миссий. Как Вы уже догадались, это
соответственно самая легкая и самая трудная миссии. Очевидно, что игру можно
закончить, не сыграв много миссий. Именно поэтому разработчики игры предложили
некоторые бонусы тем, кто сможет сыграть наибольшее количество миссий. И
поверьте, бонусы стоят того. Вы получите больше здоровья, оружия и других вещей
для победы!
Для
заинтересованных игроков существуют еще более потрясающие новости. Пусть K –
максимальное количество миссий, которое может быть закончено, когда игрок
завершает игру первый раз. Если кто-то сможет пройти игру несколько раз (начиная
с первой миссии и заканчивая последней) таким образом, что в точности K миссий
будет завершено каждый раз за игру, и при этом будет сыграно наибольшее
количество игр при заданных ограничениях, то игрок получит бесконечное
количество оружия и непобедимость. И это еще не все; все миссии будут открыты
для игрока. А это значит, что будут и бесконечное оружие, бесконечное здоровье,
а также бесконечное число хороших парней в Вашей власти.
Ваша задача
проста и очевидна. Необходимо заинтересованному игроку помочь выбрать
максимальное количество миссий, которое можно закончить при заданных
ограничениях. Порядок миссий в каждой игре важен, он должен строиться согласно
сюжетной линии.
Вход. Первая строка содержит значение n (1 < n ≤ 100). Каждая из
следующих n строк содержит
название миссии и уровень ее сложности. Название миссии содержит до 20 символов,
а уровень сложности характеризует положительное целое число. Символы в названии
миссии чувствительны к регистру, и могут содержать только буквы, числа и символ
подчеркивания. Уровень сложности не более 108. Название миссии не
дублируется.
Выход. Вывести максимальное количество миссий,
которое может быть завершено при заданных ограничениях. Это число не должно
включать в себя первую и последнюю миссию.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 Rob_The_Cop
6 A_Petty_Thief
5 Meet_The_Boss
3 |
3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 Meet_The_Boss
3 Rob_The_Cop
6 A_Petty_Thief
5 |
2 |
РЕШЕНИЕ
графы –
максимальный поток
Анализ алгоритма
Вычисляем значение К – длину наибольшей возрастающей
подпоследовательности (НВП). При этом для каждого элемента входной
последовательности в массиве g фиксируем, на каком месте НВП он может
находиться (g[i] содержит позицию в
НВП, в которой может находиться i-ая
миссия).
Дальше строим многоярусную сеть (multistage network) с К
ярусами, пронумерованных от 0 до К – 1. В один ярус включаются те элементы,
которые могут находиться на одном и том же месте НВП. Каждому элементу ставим в
соответствие две вершины графа, соединенные ребром как показано ниже в примере.
Разделение миссии на две вершины необходимо для того, чтобы она могла быть
сыграна не более одного раза. Ребра ведут только от элементов одного яруса к
строго меньшим элементам соседнего левого яруса, причем первые должны
находиться правее вторых в последовательности миссий (миссии, сыгранные в одной
игре, должны образовывать подпоследовательность в исходной последовательности).
Вводим две дополнительные вершины: исток и сток. Из истока ребра идут в
вершины, соответствующие элементам, которые могут находиться на К - ом месте
НВП ((К – 1) - ый ярус), а из элементов, которые могут находиться на первом
месте НВП (нулевой ярус), ребра идут в сток. Все ребра ориентированные, их
пропускная способность равна 1.
Ответом задачи будет величина максимального потока
построенной сети, умноженная на длину НВП (число К).
Пример
Построим граф,
соответствующий следующему тесту:
5
a1
4
a2
2
a3
7
a4
3
a5
1
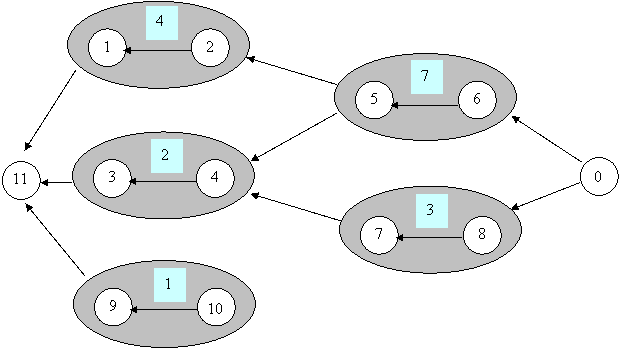
Состояние массива g равно (0, 0, 1, 1, 0). Первая, вторая и
пятая миссии находятся на нулевом ярусе сети, а вторая и третья на первом.
Нумерация миссий начинается с нуля.
Длина НВП равна К = 2. Максимальный поток из вершины 0 в
вершину 11 равен 2. То есть можно сыграть 2 игры, каждая из которых состоит из
2 миссий. Заинтересованный игрок в целом сыграет 2 * 2 = 4 миссии.
Реализация алгоритма
Сложность миссий
в паре с их названиями храним в векторе пар v.
Многоярусная сеть представляется в виде матрицы смежности m. Истоком является
вершина с номером 0. Миссии с номером i
соответствуют две вершины графа 2i и
2i – 1. Если всего имеется n миссий, то вершина - сток имеет номер
2n + 1.
#define MAX 210
vector<pair<int,string> > v;
int m[MAX][MAX], used[MAX];
vector<int> g;
Запускаем
алгоритм вычисления наибольшей возрастающей подпоследовательности (НВП). По
завершению функции LIS длина НВП содержится в переменной k. Для каждой миссии в массиве g запоминаем, на каком месте НВП она
может находиться.
void LIS(vector<pair<int,string>
> &v)
{
int i, pos;
vector<int> lis(v.size(),0);
g.resize(v.size());
for (k = i = 0; i < v.size(); i++)
{
pos = lower_bound(lis.begin(),lis.begin()+k,v[i].first) –
lis.begin();
lis[pos] = v[i].first;
if (pos == k) k++;
Миссия i в НВП может
находиться на позиции pos.
g[i] = pos;
}
}
Ищем максимальный поток в графе.
int aug(int x,int t,int CurFlow)
{
if (x == t) return
CurFlow;
if (used[x]++) return
0;
for (int Flow, y = 0;
y <= 2 * n + 1; y++)
{
if (m[x][y] > 0 && (Flow =
aug(y,t,min(CurFlow,m[x][y]))))
{
m[x][y] -= Flow; m[y][x] += Flow;
return Flow;
}
}
return 0;
}
Основная часть
программы. Читаем входные миссии и заносим их в массив v.
scanf("%d\n",&n);
v.clear(); g.clear();
for(i = 0; i < n; i++)
{
scanf("%s %d\n",s,&t);
v.push_back(make_pair(t,(string)s));
}
Запускаем алгоритм построения НВП. Строим массив g.
LIS(v);
memset(m,0,sizeof(m));
Строим многоярусную сеть. Проводим ориентированное ребро
между двумя вершинами одной миссии (от вершины 2i к 2i – 1).
for(i = 1; i <= n; i++) m[2*i][2*i-1] = 1;
Проведем ребра из вершин нулевого яруса в сток, которому
соответствует вершина номер 2n +1.
Если для i-ой миссии значение g[i – 1] равно нулю, то i-ая миссия находится на нулевом ярусе,
и от нее (вершины 2i – 1) следует
провести ребро в сток.
for(i = 1; i <= g.size(); i++)
if (g[i-1] == 0) m[2*i-1][2*n+1] = 1;
Проведем ребра из истока 0 в вершины (k – 1)-го яруса.
for(i = 1; i <= g.size(); i++)
if (g[i-1] == k - 1) m[0][2*i] = 1;
j-ая миссия
играется после i-ой. Сложность j-ой миссии должна быть больше i-ой.
j-ая миссия должна находиться в НВП на одну позицию дальше i-ой. Если это так, то проводим
ориентированное ребро между миссиями (строим ребра между ярусами).
for(i = 0; i < g.size(); i++)
for(j = i + 1; j < g.size(); j++)
if ((v[i].first < v[j].first)
&& (g[i] == g[j] - 1))
m[2*(j+1)-1][2*(i+1)] = 1;
Ищем максимальный поток на построенной сети.
MaxFlow = 0;
do
{
memset(used,0,sizeof(used));
} while ((flow =
aug(0,2*n+1,0x7FFFFFFF)) && (MaxFlow += flow));
Максимальное количество миссий, которое может быть завершено,
равно величине максимального потока MaxFlow,
умноженному на длину k НВП.
printf("%d\n",k*MaxFlow);