1111. Функция Аккермана
Как известно,
функция Аккермана играет важную роль в теоретической информатике. Однако, с
другой стороны, её быстрый рост вызывает трудности при вычислении.
Функция
Аккермана может быть определена рекурсивно для неотрицательных целых чисел m
и n следующим образом:
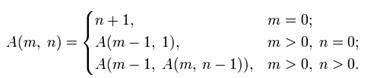
По заданным m
и n вычислите значение A(m, n).
Вход. В каждой строке входных данных
находятся два неотрицательных целых числа m и n, где 0 ≤ m
≤ 3. Для всех m < 3 значение n не превышает 1000000,
если же m = 3, то значение n не превышает 24.
Выход. Для
каждой заданной пары чисел выведите в отдельной строке искомое значение функции
Аккермана A(m, n).
|
Пример входа |
Пример выхода |
|
1 3 2 4 |
5 11 |
РЕШЕНИЕ
математика
Анализ алгоритма
Если m =
0, то A(0, n) = n + 1. Что следует из условия.
Если m =
1, то A(1, n) = A(0, A(1, n – 1)) = A(1, n – 1) + 1 = A(1,
n – 2) + 2 = … = A(1, 0) + n = A(0, 1) + n = 2 + n.
Если m =
2, то A(2, n) = A(1, A(2, n – 1)) = A(2, n – 1) + 2 = A(2,
n – 2) + 4 = … = A(2, 0) + 2n
= A(1, 1) + 2n = 2 + 1 + 2n = 2n
+ 3.
Если m =
3, то A(3, n) = A(2, A(3, n – 1)) = 2 * A(3, n – 1) + 3 =
2 * (2 * A(3, n – 2) + 3) + 3 = 4 * A(3, n – 2) + 3*2 + 3 = 8 *
A(3, n – 3) + 3*4 + 3*2 + 3 = … = 2n * A(3, 0) + 3*2n–1
+ … + 3*4 + 3*2 + 3 = 2n * A(2, 1) + 3*(2n
– 1) = 2n * (2*1 + 3) + 3*2n – 3 = 2n+3
– 3.
Итак, имеем
следующий набор формул:
A(0, n)
= n + 1,
A(1, n)
= n + 2,
A(2, n)
= 2n + 3,
A(3, n)
= 2n+3 – 3
Реализация алгоритма
Читаем входные данные. В
зависимости от значения m вычисляем ответ по одной из приведенных в
анализе задачи формул.
while(scanf("%lld
%lld",&m,&n) == 2)
{
if (m == 0)
res = n + 1; else
if (m == 1)
res = n + 2; else
if (m == 2)
res = 2*n + 3; else res = (1 << (n + 3))
- 3;
printf("%lld\n",res);
}
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long res;
while(con.hasNextLong())
{
long m = con.nextLong();
long n = con.nextLong();
if (m == 0) res = n + 1; else
if (m == 1) res = n + 2; else
if (m == 2) res = 2*n + 3; else
res = (1 << (n + 3)) - 3;
System.out.println(res);
}
con.close();
}
}