1121. A^B mod C

По заданным a, b, c вычислите значение a^b mod c (1 ≤ a, b, c < 2⁶³).

Вход. Состоит из нескольких тестов. Каждый тест задается в одной строке и содержит три числа a, b, c.

Выход. Для каждого теста в отдельной строке вывести результат выполнения операции a^b mod c.

Пример входа	Пример выхода
3 2 4 2 10 1000	1 24

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Поскольку значение степени b велико, следует воспользоваться алгоритмом возведения в степень с оценкой O(log₂b).

Пусть f(n) = aⁿ, где n – некоторая константа. Тогда имеет место соотношение:

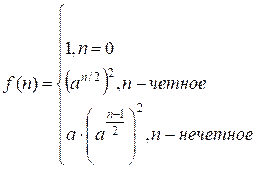
Реализация алгоритма

Работать будем с беззнаковым 64-битовым целочисленным типом.

typedef unsigned long long ull;

Умножение двух 63-битовых чисел, взятое по модулю: ab mod c. Во избежании реализации длинной арифметики, мы можем воспользоваться при умножении только одним дополнительным 64-ым битом.

Пусть b₁b₂b₃…b_k – двоичное представление числа b. Тогда произведение ab можно расписать как сумму ab_k + 2ab_k-1 + 4ab_k-2 + … + 2^k-1ab₁.

ull mult(ull a, ull b, ull c)

{

ull res = 0;

a = a % c;

while (b)

{

if (b & 1)

{

res += a;

if (res > c) res -= c;

}

a <<= 1;

if (a > c) a -= c;

b >>= 1;

}

return res;

}

Вычисление a^b mod c согласно приведенной в анализе задачи рекуррентности.

ull pow(ull a, ull b, ull c)

{

ull temp;

if (b == 0) return 1;

temp = pow(a,b/2,c);

if (b % 2 == 0)

return mult(temp,temp,c);

else

return mult(mult(temp,temp,c),a,c);

}

Основная часть программы.

while(scanf("%llu %llu %llu",&a,&b,&c) == 3)

{

a = a % c;

if (a == 1) res = 1; else res = pow(a,b,c);

printf("%llu\n",res);

}

Реализация алгоритма – (a * b) % c рекурсивная

Воспользуемся следующим рекуррентным соотношением для вычисления произведения двух чисел:

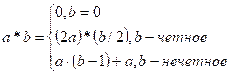
#include <stdio.h>

typedef unsigned long long ull;

ull a, b, c, res;

// (a * b) mod c

ull mult(ull a, ull b, ull c)

{

if (b == 0) return 0;

if (b % 2 == 0)

return mult((2 * a) % c, b / 2, c);

return (mult(a, b - 1, c) + a) % c;

}

ull pow(ull a, ull b, ull c)

{

ull temp;

if (b == 0) return 1;

temp = pow(a,b/2,c);

if (b % 2 == 0)

return mult(temp,temp,c);

else

return mult(mult(temp,temp,c),a,c);

}

int main(void)

{

while(scanf("%llu %llu %llu",&a,&b,&c) == 3)

{

a = a % c;

if (a == 1) res = 1; else res = pow(a,b,c);

printf("%llu\n",res);

}

return 0;

}

Java реализация

import java.util.*;

import java.math.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(con.hasNext())

{

BigInteger a = con.nextBigInteger();

BigInteger b = con.nextBigInteger();

BigInteger c = con.nextBigInteger();

BigInteger res = a.modPow(b,c);

System.out.println(res);

}

con.close();

}

}

Python реализация

import sys

for s in sys.stdin:

x, n, m = map(int,s.split())

print(pow(x, n, m))

Python реализация – функция

def Pow(x, n, m):

if (n == 0): return 1

if (n % 2 == 0): return Pow((x * x) % m, n // 2, m)

return (x * Pow(x, n - 1, m)) % m

import sys

for s in sys.stdin:

x, n, m = map(int,s.split())

print(Pow(x, n, m))