1128. Longge’s problem

 

Longge is good at mathematics, and he likes to think about hard mathematical problems which will be solved by some graceful algorithms. Now a problem comes:

Given an integer n. Compute ∑gcd(i, n) for all 1 ≤ i ≤ n.

“Oh, I know, I know!” Longge shouts! But do you know? Please solve it.

 

Input. Each line contains one number n (1 < n < 231).

 

Output. For each number n print in a separate line the sum ∑gcd(i, n) for all 1 ≤ i ≤ n.

 

Sample input

Sample output

2

6

12

3

15

40

 

 

SOLUTION

number rtheory

 

Algorithm analysis

Theorem. If the function f(n) is multiplicative, then the summation function Sf(n) =  is also multiplicative.

► Let x, y Î N, where x and y are coprime. Let x1, x2, …, xk be all divisors of x. Let y1, y2, …, ym be all divisors of y. Then GCD(xi, yj) = 1, and all possible products xiyj give all divisors of xy. Then

Sf (x) * Sf 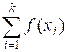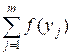(y) =  *  =  =  = Sf (xy)

 

Corollary. Consider the function f(n) = GCD(n, c), where c is a constant. If x and y are coprime, then f(x * y) = GCD(x * y, c) = GCD(x, c) * GCD(y, c) = f(x) * f(y). Therefore the function f(n) = GCD(n, c) is multiplicative.

Let g(n) = 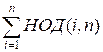. Then

g() = g() * g() * … * g()

 

Theorem. For any prime p and positive integer a holds the relation:

g(pa) = (a + 1)pa – apa–1 

► For à = 1 we have:

g(p) = GCD(1, p) + GCD(2, p) + … + GCD(p, p) = (p – 1) + p = 2p – 1

 

Similarly for à = 2:

 

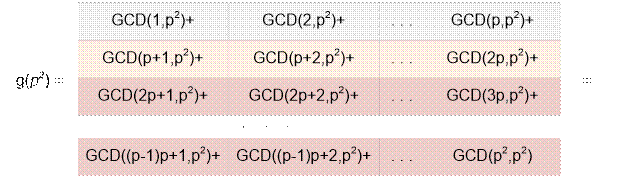
= (1 + 1 + … + 1 + p) +

(1 + 1 + … + 1 + p) +

…

(1 + 1 + … + 1 + p2) =

 

= (p – 1 + p) * (p – 1) + (p – 1 + p2) =

(2p – 1) * (p – 1) + (p2 + p – 1) =

2p2 – 2p – p + 1 + (p2 + p – 1) =

= 3p2 – 2p

 

Lemma. If d is a divisor of n, then there are exactly  numbers i such that GCD(i, n) = d.

► Obviously i must be divisible by d, let i = dj. Then

GCD(i, n) = GCD(dj, n) = d * GCD(j, n / d)

If the last expression is equal to d, then GCD(j, n / d) = 1. The number of such j that GCD(j, n / d) = 1 is .

 

Example. The number of such i that GCD(i, 24) = 3 is  = 4.

GCD(j, 8) = 1 for j Î {1, 3, 5, 7}, therefore GCD(i, 24) = 3 for i Î {3, 9, 15, 21} (we have i = 3j).

 

Theorem.

g(n) =  =

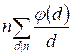
► According to the above lemma, the number of pairs (i, n) for which GCD(i, n) = e, is exactly . Replacing n / e = d, we get:

g(n) =  =  =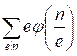

 

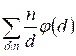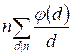
Example. Let n = 6.

Then g(6) =  =

= GCD(1, 6) + GCD(2, 6) + GCD(3, 6) + GCD(4, 6) + GCD(5, 6) + GCD(6, 6) =

= 1 + 2 + 3 + 2 + 1 + 6 = 15

In the same time g(6) = g(2) * g(3) =

(GCD(1, 2) + GCD(2, 2)) * (GCD(1, 3) + GCD(2, 3) + GCD(3, 3)) =

(1 + 2) * (1 + 1 + 3) = 3 * 5 = 15

 

Compute g(6) using the formula g(n) = :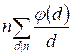

g(6) = =   =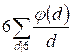

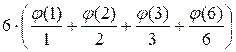=  = 6 + 3 + 4 + 2 = 15

 

Let’s calculate g(6) based on the multiplicativity of the function f(x) = GCD(x, n):

g(6) = g(2) * g(3) = (2*2 – 1) * (2*3 – 1) = 3 * 5 = 15

 

Example. Let n = 12. Then g(12) =  =

1 + 2 + 3 + 4 + 1 + 6 + 1 + 4 + 3 + 2 + 1 + 12 = 40

 

In the same time g(12) = g(4) * g(3) =

(GCD(1, 4) + GCD(2, 4) + GCD(3, 4) + GCD(4, 4)) *

* (GCD(1, 3) + GCD(2, 3) + GCD(3, 3)) =

(1 + 2 + 1 + 4) * (1 + 1 + 3) = 8 * 5 = 40

 

Compute g(12) using the formula g(n) = :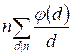

g(12) = =   =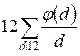

=  =

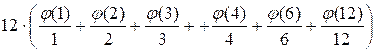= 12 + 6 + 8 + 6 + 4 + 4 = 40

 

The divisors of 12 are: 1, 2, 3, 4, 6, 12. The number of i such that GCD(i, 12) = d equals to . For example GCD(i, 12) = 3 holds for  =  = 2 different i, namely for i = 3, 9.

 

Let’s calculate g(12) based on the multiplicativity of the function f(x) = GCD(x, n):

g(12) = g(22) * g(3) = (3 * 22 – 2 * 2) * (2*3 – 1) = 8 * 5 = 40

 

Algorithm realization

Function euler computes the Euler function.

 

long long euler(long long n)

{

  long long i, result = n;

  for (i = 2; i * i <= n;i++)

  {

    if (n % i == 0) result -= result / i;

    while (n % i == 0) n /= i;

  }

  if (n > 1) result -= result / n;

  return result;

}

 

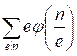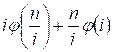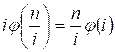The main part of the program. Read value of n. Compute the value g(n) by the formula . Search for all divisors of n among the numbers from 1 to . If i is a divisor of n, then n / i will be also the divisor of n. Therefore, for each found divisor i ≤  we must add to result res the value . If n is a full square, i = sq = , then  and two identical terms will be added to the res sum. Therefore we’ll subtract one of them from res during the initialization of the variable.

 

while(scanf("%lld",&n) == 1)

{

  sq = (long long)sqrt(1.0*n);

  res = (sq * sq == n) ? -sq * euler(sq) : 0;

  for(i = 1; i <= sq; i++)

    if(n % i == 0) res = res + i * euler(n/i) + (n / i) * euler(i);

  printf("%lld\n",res);

}

 

Realization taking into account the multiplicativity

 

#include <stdio.h>

#include <math.h>

 

long long i, n, res, a, p;

 

int main(void)

{

  while(scanf("%lld",&n) == 1)

  {

    res = 1;

    for(i = 2; i * i <= n; i++)

    {

      if(n % i == 0)

      {

        a = 0; p = 1;

        while(n % i == 0)

        {

          a++;

          p *= i;

          n /= i;

        }

        res *= (a + 1) * p - a * p / i;

      }

    }

    if (n > 1) res *= (2*n - 1);

    printf("%lld\n",res);

  }

  return 0;

}

 

Java realization

 

import java.util.Scanner;

 

public class Main

{

  static long euler(long n)

  {

    long result = n;

    for(int i = 2; i <= Math.sqrt(n);i++)

    {

      if (n % i == 0) result -= result / i;

      while (n % i == 0) n /= i;

    }

    if (n > 1) result -= result / n;

    return result;

  }

   

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

    while(con.hasNext())

    {

      long n = con.nextLong();

      long sq = (long)Math.sqrt(n);

      long res = (sq * sq == n) ? -sq * euler(sq) : 0;

      for(long i = 1; i <= sq; i++)

        if (n % i == 0)

          res = res + i * euler(n/i) + (n / i) * euler(i);

      System.out.println(res);

    }

    con.close();

  }

}