1155. Задача Евклида
Со времен
Евклида известно, что для любых положительных a и b существуют
такие целые x и y, что ax + by = d, где d
– наибольший общий делитель a и b. По заданным a и b
найти x, y, d.
Вход. Каждая строка содержит два натуральных числа
a и b, разделенных пробелом (a, b £ 109).
Выход. Для каждой пары a и b в отдельной строке
вывести три целых числа x, y и d,
разделенных пробелом. Если искомых значений x
и y несколько, то следует выводить
такую пару, для которой |x| + |y| минимально. Если и таких пар
несколько, то вывести ту пару, в которой x
минимально.
|
Пример входа |
Пример выхода |
4 6
17 17 5 3 |
-1 1 2
0 1 17 -1 2 1 |
РЕШЕНИЕ
расширенный
алгоритм Евклида
Анализ алгоритма
Рассмотрим уравнение: 7x + 9y
= 1, где GCD(7, 9) = 1. Вам следует найти такую пару (x, y), для которой |x|
+ |y| минимально. Ответом будет (x, y)
= (4, -3), так как 7 * 4 + 9 * (-3) = 1.
Пусть для положительных целых чисел a
и b (a > b) известны d = НОД(a, b) = НОД(b, a % b),
а также числа x’ и y’, для которых
d = b * x’ + (a % b) * y’
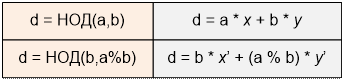
Поскольку a % b
= a – ![]() * b, то
* b, то
d = b * x’ + (a – ![]() * b) * y’ = a *
y’ + b * (x’
–
* b) * y’ = a *
y’ + b * (x’
– ![]() * y’) = a * x
+ b * y,
* y’) = a * x
+ b * y,
где обозначено x = y’, y
= x’ – ![]() * y’.
* y’.
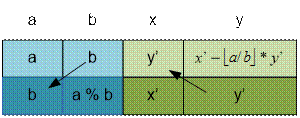
Пусть gcdext(int
a, int
b, int
&d, int &x, int &y) –
функция, которая по входным числам a и b находит d = НСД(a,
b) и такие x, y что d = a * x + b
* y. Для поиска неизвестных x
и y необходимо рекурсивно запустить
функцию gcdext(b, a mod b, d, x, y)
и пересчитать значения x и y по выше приведенной формуле.
Рекурсия заканчивается, когда b = 0. При b = 0 НОД(a, 0) =
a и a = a * 1 + 0 * 0, поэтому полагаем x = 1, y
= 0.
Пример
Рассмотрим
третий тест. Вычисление НОД(5, 3) и нахождение соответствующих значений x и y
произведем в таблице:
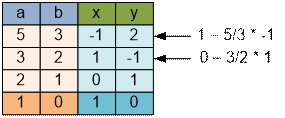
Из таблицы
находим, что НОД(5, 3) = 5 * (-1) + 3 * 2 = 1.
Найдем решение
уравнения 5x + 7y
= 1.
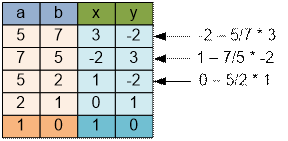
Ответ имеет вид:
НОД(5, 7) = 5 * 3 + 7 * (-2) = 1.
Реализация
алгоритма
Функция gcdext по заданным a и b находит
такие значения x, y, d, что ax + by = d,
используя расширенный алгоритм Евклида.
void gcdext(int a, int b, int &d, int &x, int &y)
{
if (b == 0)
{
d = a; x = 1; y = 0;
return;
}
gcdext(b, a % b, d, x, y);
int s = y;
y = x - (a / b) * y;
x = s;
}
Основная часть
программы. Обрабатываем несколько тестов. Читаем входные данные.
while(scanf("%d
%d",&a,&b) == 2)
{
Вызываем функцию
gcdext и выводим результат.
gcdext(a,b,d,x,y);
printf("%d %d
%d\n",x,y,d);
}
Java реализация
import java.util.*;
public class Main
{
static int[] GcdExtended(int a, int b)
{
int res[] = new int[3]; // d, x, y
if (b == 0)
{
res[0] = a; res[1] = 1; res[2] = 0;
return res;
}
res = GcdExtended(b,a % b);
int s = res[2];
res[2] = res[1] - (a / b) * res[2];
res[1] = s;
return res;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while(con.hasNext())
{
int a = con.nextInt(), b = con.nextInt();
int res[] = GcdExtended(a,b);
System.out.println(res[1] + " " + res[2] + " " + res[0]);
}
}
}