1181. Монетный завод

Канадский королевский монетный двор получил заказ на изготовление столиков для кофе, ножки которых представляют собой купы монет. Каждый стол имеет четыре ножки, в каждой ножке используются монеты одинакового номинала, но при этом все номиналы в четырех ножках различны. Например, одна ножка может состоять из 25 центовых монет, другая из одноцентовых, еще одна ножка из двухцентовых монет. Высоты всех ножек должны быть одинаковыми.

Много монет доступно для изготовления таких ножек, включая памятные и иностранные. Вам известны имеющиеся в наличии номиналы монет и желаемая высота стола. Какую ближайшую к желаемой длину могут иметь сконструированные ножки, если каждая из них должна строится из уникального номинала монет?

Вход. Состоит из нескольких тестов. Каждый тест начинается следующими целыми числами: количество имеющихся номиналов монет n (4 ≤ n ≤ 100) и количество столов t (1 ≤ t ≤ 10), которое следует сделать. Далее следуют n строк; каждая из них характеризует толщину номинала монет в сотых миллиметра. Каждая из следующих t строк описывает высоту желаемого стола (также в сотых миллиметра). Последняя строка содержит 0 0 и означает конец входных данных.

Выход. Для каждого стола вывести два целых числа: наибольшую длину ножек, не превосходящую желаемую высоту, и наименьшую длину ножек, не меньшую желаемой высоты.

Пример входа	Пример выхода
4 2 50 100 200 400 1000 2000 0 0	800 1200 2000 2000

РЕШЕНИЕ

НОК

Анализ алгоритма

Если a, b, c, d – толщины четырех типов монет, то минимально возможная высота стола, который можно сделать, равна h = НОК(a, b, c, d). Обозначим через low максимально возможную высоту стола, не большую желаемой величины Height. Тогда low должно делиться на h и быть максимально возможным значением, не большим Height. Отсюда

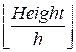low = * h

Если вычисленное low равно Height (что возможно в случае, когда Height делится на h без остатка), то минимально возможная высота стола more, не меньшая Height, также равна Height. Иначе она равна low + h.

Остается перебрать все возможные четверки толщин номиналов монет и вычислить максимум среди всевозможных low и минимум среди всевозможных more.

Пример

Рассмотрим набор монет из первого теста, желаемая высота стола равна 1000. Имея 4 монеты с толщинами 50, 100, 200, 400 можно конструировать столы, высоты которых кратны НОК(50, 100, 200, 400) = 400. Искомые высоты столов, которые можно сделать, соответственно равны 800 и 1200.

Реализация алгоритма

Для решения задачи достаточно использовать целочисленный тип int. Поскольку на вход подается несколько тестов, читаем в цикле входные значения n и t, а также значения номиналов монет текущего теста в массив coins.

while(scanf("%d %d",&n,&t),n + t > 0)

{

for(i = 0; i < n; i++) scanf("%d",&coins[i]);

Для каждой прочитанной желаемой высоты стола Height применяем описанный выше алгоритм. Обозначим через Less максимум среди всевозможных low, а через Greater – минимум среди всевозможных more. Проинициализируем их.

while(t--)

{

scanf("%d",&Height);

Greater = 0x7FFFFFFF;

Less = 0;

Перебираем все возможные четверки номиналов монет x1 < x2< x3 < x4 (номиналы монет хранятся соответственно в coins[x1], coins[x2], coins[x3], coins[x4]).

for(x1 = 0; x1 < n - 3; x1++)

for(x2 = x1 + 1; x2 < n - 2; x2++)

for(x3 = x2 + 1; x3 < n - 1; x3++)

for(x4 = x3 + 1; x4 < n; x4++)

{

Вычисляем НОК толщин монет g = НОК(coins[x1], coins[x2], coins[x3], coins[x4]).

h = coins[x1] * coins[x2] / gcd(coins[x1],coins[x2]);

h = h / gcd(h,coins[x3]) * coins[x3];

h = h / gcd(h,coins[x4]) * coins[x4];

Для каждой четверки номиналов пересчитываем значения Less и Greater.

low = Height / h * h;

if (low > Less) Less = low;

if (low != Height) low += h;

if (low < Greater) Greater = low;

}

Выводим результат:

printf("%d %d\n",Less,Greater);

}

}