1184. Гипер - устройство
Гипер-устройство
- это часто используемый термин в научно-фантастических рассказах. Хотя многие
считают, что гипер-устройство не возможно, тем не менее существует большое
количество теорий, описывающих черные дыры и гипер-устройства. Говорят, что
гипер-устройство позволяет путешествовать в более высоких измерениях. В этой
задаче Вас следует вычислить стоимость путешествия по большим измерениям
согласно теории старого сумасшедшего друга Арифа. Я уверен, что вы знаете кто
такой Ариф. Если нет, то можете спросить у своих товарищей по команде.
Пусть P и Q
– две точки в n мерном пространстве,
координаты которых соответственно равны P(p1, p2, …, pn)
и Q(q1, q2,
…, qn).
Универсальное n-мерное пространство
разбито на маленькие единичные n-мерные
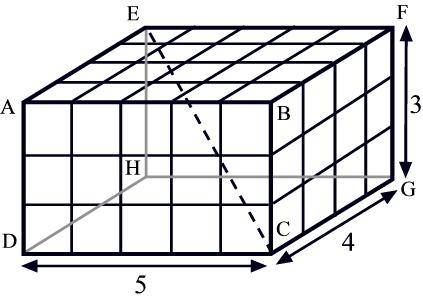
гиперкубы. Для наглядного примера представленное ниже (5 x 4 x 3) трехмерное
пространство разбито на 60 трехмерных единичных кубов (1 x 1 x 1).
Давайте
обойдемся без визуализации примеров в больших размерностях. Стоимость
путешествия от одной n-мерной точки P
до другой n-мерной точки Q равна
"количеству разных n-мерных
единичных гиперкубов, которое пересекает отрезок, соединяющий эти две
точки". Вам следует вычислить эту стоимость. Например, на рисунке сверху
стоимость путешествия от C до E равно 10 единицам, так как отрезок EC проходит
через 10 разных единичных трехмерных гиперкубов.
Вход. Первая строка содержит количество тестов n (n
≤ 501). Каждый тест начинается целым числом D (0 < D ≤ 10) –
размерностью, в которой будет измеряться стоимость. Каждая из следующих двух
строк содержит D целых чисел. D чисел первой строки задают координаты P, а D
чисел второй строки задают координаты Q.
Все числа положительны и являются 32-битовыми знаковыми целыми.
Выход. Для каждого
теста вывести в одной строке стоимость путешествия из P в Q, которая является
целым числом.
|
Пример
входа |
Пример
выхода |
|
2 2 10 10 10 13 1 10 20 |
Case 1: 0 Case 2: 10 |
РЕШЕНИЕ
комбинаторика, принцип включения –
исключения, НОД
Анализ алгоритма
Построим вектор d = (|p1 – q1|,
|p2 – q2|, …, |pn
– qn|) = (d1, d2, …, dn).
Ответ res можно вычислить, используя
формулу включения - исключения.
Если d = (d1,
d2), то res = d1 + d2
– gcd(d1, d2).
Если d = (d1,
d2, d3), то res =
d1 + d2 + d3 – gcd(d1, d2)
– gcd(d1, d3) – gcd(d2, d3) + gcd(d1,
d2, d3).
Реализация алгоритма
Считываем
входные данные для каждого теста.
scanf("%lld",&n);
for(test = 0; test < n; test++)
{
scanf("%lld",&dim);
for(i = 0; i
< dim; i++) scanf("%lld",&a[i]);
for(i = 0; i
< dim; i++) scanf("%lld",&b[i]);
Вычисляем массив
d = (|p1 – q1|,
|p2 – q2|, …, |pn
– qn|) = (d1, d2, …, dn).
for(i = 0; i
< dim; i++)
d[i] = (a[i] >
b[i]) ? a[i] - b[i] : b[i] - a[i];
res = 0;
Перебираем все подмножества множества
{d1, d2, …, dn}. Каждое подмножество генерируется
по числу i (1 £ i
£ 2dim – 1), выбирая из его двоичного представления
позиции, на которых стоят единицы.
for(i = 1; i
< 1<<dim; i++)
{
ptr = temp = cnt = 0; j = i;
while(j
> 0)
{
if (j %
2)
{
temp = gcd(temp,d[ptr]);
cnt++;
}
ptr++; j /= 2;
}
Если подмножество состоит из четного
количества элементов, то НОД его элементов вычитается их общего результата.
Если из нечетного – то прибавляется.
res += (cnt % 2) ? temp : -temp;
}
Выводим результат
printf("Case
%lld: %lld\n",test+1,res);
}