12195. Чинар – символ Азербайджана

Вы же знаете, что у каждой страны есть своё дерево-символ? В Греции это олива, в Японии – сакура, в Канаде – клён, в Австралии – золотая акация (мимоза), в России и Финляндии – берёза.

А дерево, которое занимает особое место в азербайджанском фольклоре и стало символом Азербайджана – это Чинар (Платан).

Чинар с древних времён окружён уважением. Ещё римляне знали и использовали его целебные свойства: отварами из плодов останавливали кровотечения, лечили ожоги и обморожения, настой из коры применяли при укусах змей. В наше время кора молодых стволов используется даже в лечении рака, а отвары и мази на основе плодов помогают при множестве заболеваний.

Представьте себе огромное дерево-чинар, выросшее в одном из парков Баку. У него n ветвей, и каждая из них окрашена либо в белый, либо в чёрный цвет. Но столь разноцветный вид нарушает его величественную гармонию. Поэтому было решено перекрасить дерево так, чтобы оно стало полностью одноцветным — либо белым, либо чёрным.

Для этого доступна лишь одна операция – paint(v), где v – это выбранная вершина дерева. Эта операция меняет цвет на противоположный у всех таких вершин u, что на кратчайшем пути от u до v все вершины имеют одинаковый цвет (при этом сами вершины u и v тоже учитываются).

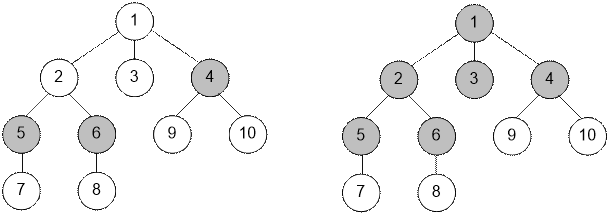
Например, дерево слева после применения операции paint(3) изменит окраску как показано справа.

Ваша задача – определить, за какое минимальное количество операций можно перекрасить чинар так, чтобы он стал полностью одноцветным.

Вход. В первой строке содержится одно целое число n (1 ≤ n ≤ 200000) –количество вершин дерева.

Во второй строке находятся n целых чисел color_i (0 ≤ color_i ≤ 1) – цвета вершин. Если color_i = 0, то i-я вершина окрашена в белый цвет, если color_i = 1, то в чёрный.

В каждой из следующих n – 1 строк записаны два целых числа u_i и v_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i) – рёбра дерева. Гарантируется, что все рёбра различны, то есть граф не содержит кратных рёбер.

Выход. Выведите одно число – минимальное количество операций перекраски, которое необходимо, чтобы чинар стал полностью белым или полностью чёрным.

Пример входа 1	Пример выхода 1
10 0 0 0 1 1 1 0 0 0 0 1 2 1 3 1 4 2 5 2 6 5 7 6 8 4 9 4 10	2
Пример входа 2	Пример выхода 2
5 0 0 0 1 1 1 2 1 3 2 4 3 5	1

РЕШЕНИЕ

дерево

Анализ алгоритма

Если две вершины одного цвета соединены ребром, их можно объединить в одну – при этом ответ не изменится. Введем понятие “компоненты связности”: две вершины принадлежат одной компоненте связности, если они:

· имеют одинаковый цвет;

· соединены между собой ребром;

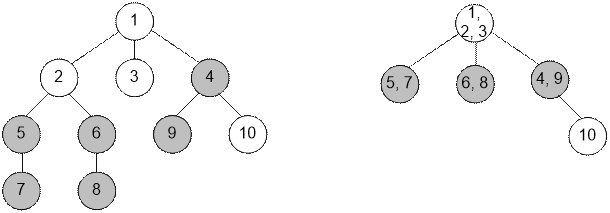
Рассмотрим, например, дерево слева. Справа отображен граф его компонент связности.

Если применить, например, операцию paint(2), то дерево компонент будет сжиматься:

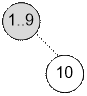
Дерево будет покрашено в один цвет тогда и только тогда, когда после таких операций покраски со “сжатием” останется ровно одна компонента.

Пусть d – диаметр дерева в графе компонент. Дерево будет покрашено в один цвет тогда и только тогда, когда диаметр дерева станет равен 0, поскольку диаметр равен 0 только у дерева, сосотоящего из одной вершины.

Найдем такую вершину, что длина кратчайшего расстояния от нее до любой другой вершины не превышает (d + 1) / 2. Такая вершина всегда найдется, поскольку иначе диаметр дерева был бы не менее d + 1. Теперь заметим, что, применив (d + 1) / 2 операций покраски к этой вершине, мы покрасим дерево в один цвет.

Реализация алгоритма

Объявим рабочие массивы.

vector<int> color, dist;

vector<vector<int> > g, g1;

vector<int> comp, used;

Функция dfs1 выполняет обход дерева в глубину и разбивает его вершины на “компоненты связности”. Каждой вершине v присваивается номер компоненты id, который сохраняется в массиве comp[v].

void dfs1(int v, int col, int id)

{

if (used[v]) return;

if (color[v] != col) return;

used[v] = 1;

comp[v] = id;

for (int to : g[v])

dfs1(to, col, id);

}

Функция dfs2 выполняет обход дерева в глубину и вычисляет расстояния от источника до каждой вершины. Для вершины v это расстояние сохраняется в dist[v]. Текущее расстояние от источника до вершины v равно d.

void dfs2(int v, int d, int p = -1)

{

dist[v] = d;

for (int to : g1[v])

if (to != p) dfs2(to, d + 1, v);

}

Основная часть программы. Читаем входные данные. Инициализируем массивы.

scanf("%d", &n);

color.resize(n + 1);

g.resize(n + 1);

comp.resize(n + 1);

used.assign(n + 1, 0);

for (i = 1; i <= n; i++)

scanf("%d", &color[i]);

Читаем и строим неориентированное дерево.

for (i = 0; i < n - 1; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

Разбиваем вершины дерева на компоненты. Общее количество компонент равно cnt. Нумерация компонент начинается с 1.

cnt = 0;

for (i = 1; i <= n; i++)

if (!used[i])

{

cnt++;

dfs1(i, color[i], cnt);

}

Строим граф g1 – граф компонент (сжатое дерево).

g1.resize(cnt + 1);

for (v = 1; v <= n; v++)

for (int to : g[v])

if (comp[v] != comp[to])

g1[comp[v]].push_back(comp[to]);

Вычисляем диаметр графа компонент.

dist.resize(cnt + 1);

Запускаем поиск в глубину из вершины 1 и заполняем массив dist, содержащий кратчайшие расстояния от этой вершины.

dfs2(1, 0, -1);

Вершина a находится на максимальном расстоянии от вершины 1.

a = max_element(dist.begin(), dist.begin() + cnt + 1) - dist.begin();

Запускаем поиск в глубину из вершины a и снова заполняем массив dist.

dfs2(a, 0, -1);

Вершина b наиболее удалена от a. Расстояние между a и b является диаметром графа компонент.

b = max_element(dist.begin(), dist.begin() + cnt + 1) - dist.begin();

Выводим ответ.

printf("%d\n", (dist[b] + 1) / 2);