12195. Chinar is a symbol of Azerbaijan
Do you know that every country has its own
symbolic tree? In Greece, it is the olive tree, in Japan – the sakura, in
Canada – the maple, in Australia – the golden wattle (mimosa), in Russia and
Finland – the birch.
The tree that holds a special place in
Azerbaijani folklore and has become a symbol of Azerbaijan is the Chinar (Plane
tree).
Since ancient times, the Chinar has been
surrounded by respect. Even the Romans knew and used its healing properties:
decoctions of its fruits stopped bleeding, treated burns and frostbites, and
infusions from its bark were used for snake bites. Nowadays, the bark of young
trunks is even used in cancer treatment, while decoctions and ointments made
from the fruits help with various ailments.
Imagine a huge Chinar tree grown in one of
the parks of Baku. It has n branches, and each branch is
colored either white or black. But such a multicolored appearance disrupts its
majestic harmony. Therefore, it was decided to repaint the tree so that it
becomes completely one color – either white or black.
Only one operation is available for
this: paint(v), where v is a chosen vertex
of the tree. This operation flips the color of all vertices u such
that on the shortest path from u to v, all
vertices have the same color (including the vertices u and v themselves).
For example, the tree on the left, after
applying the operation paint(3), will change its coloring as shown
on the right.
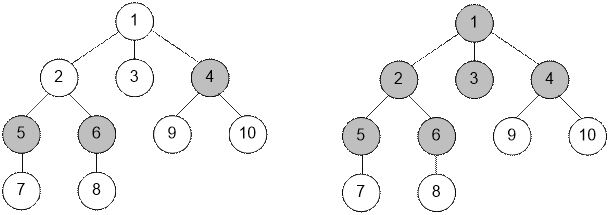
Your task is to determine the minimum
number of operations required to repaint the Chinar so that it becomes entirely
one color.
Input. The first line contains a single integer n (1 ≤ n ≤ 200000) – the number of vertices of the tree.
The second line contains n integers colori (0 ≤ colori ≤
1) – the colors of the
vertices. If colori = 0, the i-th
vertex is white; if colori = 1, it is black.
Each of the following n – 1 lines contains two integers ui and vi (1 ≤ ui, vi
≤ n, ui ≠ vi) – the edges of the tree. It is guaranteed
that all edges are distinct, so the graph contains no multiple edges.
Output. Print a single integer –
the minimum number of repaint operations required to make the Chinar completely
white or completely black.
|
Sample input 1 |
Sample output
1 |
|
10 0 0 0 1 1 1 0 0 0 0 1 2 1 3 1 4 2 5 2 6 5 7 6 8 4 9 4 10 |
2 |
|
|
|
|
Sample input 2 |
Sample output
2 |
|
5 0 0 0 1 1 1 2 1 3 2 4 3 5 |
1 |
SOLUTION
tree
Algorithm analysis
If two vertices
of the same color are connected by an edge, they can be merged into one – the answer will
remain unchanged. Let’s introduce the concept of a connected component: two
vertices belong to the same connected component if they
·
have the same color, and
·
are connected by an edge.
Consider, for example, the
tree on the left. On the right, the graph of its connected components is shown.
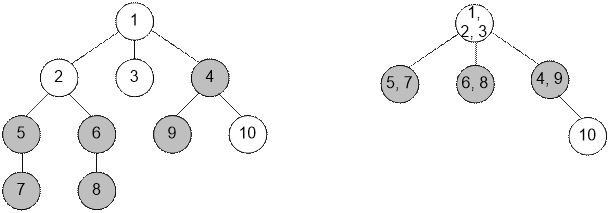
If we apply, for example,
the operation paint(2), the component tree will be compressed:
The tree will be
painted in a single color if and only if, after such painting operations with
compression, exactly one component remains.
Let d be
the diameter of the component tree. The tree will be painted in a single color
if and only if the diameter of the tree becomes 0, since a diameter of 0 occurs
only in a tree consisting of a single vertex.
We now find such
a vertex that the length of the shortest path from it to any other vertex does
not exceed (d + 1) / 2. Such a vertex always exists, because otherwise
the diameter of the tree would be at least d + 1.
Finally, note
that by applying (d + 1) / 2 painting operations to this vertex, we can
paint the entire tree in a single color.
Algorithm implementation
Define the arrays.
vector<int> color, dist;
vector<vector<int> > g, g1;
vector<int> comp, used;
The function dfs1 performs a depth-first traversal of the
tree and partitions its vertices into connected components. Each vertex v
is assigned a component number id, which is stored in the array comp[v].
void dfs1(int v, int col, int id)
{
if (used[v]) return;
if (color[v] != col) return;
used[v] = 1;
comp[v] = id;
for (int to : g[v])
dfs1(to, col, id);
}
The function dfs2 performs a depth-first traversal of the
tree and computes the distances from the source to each vertex. For a vertex v,
this distance is stored in dist[v]. The current distance from the source
to vertex v is denoted by d.
void dfs2(int v, int d, int p = -1)
{
dist[v] = d;
for (int to : g1[v])
if (to != p) dfs2(to, d + 1, v);
}
The main part of the program. Read the input data and initialize the
arrays.
scanf("%d", &n);
color.resize(n
+ 1);
g.resize(n
+ 1);
comp.resize(n
+ 1);
used.assign(n
+ 1, 0);
for (i = 1; i <= n; i++)
scanf("%d", &color[i]);
Read and construct an undirected tree.
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Partition the vertices of the tree into components. The total number of
components is cnt. The components are numbered starting from 1.
cnt = 0;
for (i = 1; i <= n; i++)
if (!used[i])
{
cnt++;
dfs1(i, color[i], cnt);
}
Construct the graph g1 – the component graph (the compressed tree).
g1.resize(cnt
+ 1);
for (v = 1; v <= n; v++)
for (int to : g[v])
if (comp[v] != comp[to])
g1[comp[v]].push_back(comp[to]);
Compute the diameter of the component graph.
dist.resize(cnt
+ 1);
Start a depth-first search from vertex 1 and fill the array dist,
which stores the shortest distances from this vertex.
dfs2(1, 0,
-1);
Vertex a is the one located at the maximum distance from vertex 1.
a =
max_element(dist.begin(), dist.begin() + cnt + 1) - dist.begin();
Start a depth-first search from vertex a and fill the array dist
again.
dfs2(a, 0,
-1);
Vertex b is the one farthest from a. The distance between a
and b is the diameter of the component graph.
b =
max_element(dist.begin(), dist.begin() + cnt + 1) - dist.begin();
Print the answer.
printf("%d\n", (dist[b] + 1) / 2);