1209. Функция с факториалами
Для
заданного четного натурального числа n вычислить значение функции
f(n) = 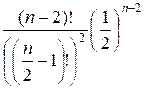
Вход. Четное натуральное число n (1
£ n £ 100000).
Выход. Значение функции f(n) с
четырьмя десятичными знаками.
|
Пример входа |
Пример выхода |
|
4 |
0.5000 |
РЕШЕНИЕ
математика
Анализ алгоритма
Прологарифмируем
равенство f(n) = 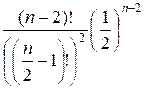 :
:
ln f(n)
= ln(n – 2)! – 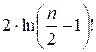 –
– ![]()
Вычислим правую
часть равенства и возведем е в нее. Получим
f(n).
Логарифм факториала вычислим как сумму логарифмов:
ln n! = ln 1 + ln 2 + ln 3 + … + ln n
Реализация алгоритма
Объявим глобальные массивы.
#define MAX 100001
double lf[MAX], ans[MAX];
Заполняем
массив lf, в котором lf[i] = lni!.
res = lf[1] = 0.0;
for(res = 0, i = 2; i < MAX; i++)
{
res += log((double)i);
lf[i] = res;
}
Заполняем
массив ans, в котором ans[i] = f(i).
for(i = 2; i < MAX; i += 2)
{
res = lf[i/2-1];
res = lf[i-2] - (i -
2) * log(2.0) - res - res; // res = ln f(i)
ans[i] =
exp(res);
}
scanf("%d",&n);
printf("%.4lf\n",ans[n]);
Java реализация
import java.util.*;
import java.io.*;
public class Main
{
public static final int MAX = 100001;
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
PrintWriter out = new PrintWriter(System.out,true);
int i, n = con.nextInt();
double lf[] = new double[MAX],
ans[] = new double [MAX];
double res = lf[1] = 0.0;
for(res = 0, i = 2; i < MAX; i++)
{
res += Math.log(i);
lf[i]
= res;
}
for(i = 2; i < MAX; i += 2)
{
res =
lf[i/2-1];
res =
lf[i-2] - (i - 2) * Math.log(2.0) - res - res;
ans[i] = Math.exp(res);
}
out.printf(Locale.US,"%.4f\n",ans[n]);
}
}