1209. ফাংশনে
ফ্যাক্টোরিয়াল
একটা
ধনাত্বক জোড়
সংখ্যা n দেওয়া
আছে। নিচের
ফাংশনটার মান
বের করতে হবে।
f(n) = 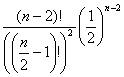
ইনপুট
ধনাত্বক
জোড় সংখ্যা n (1 £ n £ 100000).
আউটপুট
f(n) এর
মান দশমিকের
পরে চার অংক
পর্যন্ত
দেখাতে হবে।
উদাহরণ
ইনপুট
4
আউটপুট
0.5000
সমাধান
গাণিতিক
অ্যালগোরিদম
অ্যানালাইসিস
f(n) = 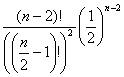 ফাংশনটার
লগারিদম নিতে
হবে।
ফাংশনটার
লগারিদম নিতে
হবে।
:
ln f(n)
= ln(n – 2)! – ![]() –
– ![]()
ডানপক্ষের
মান বের করতে
হবে এবং åডানপক্ষ বের
করতে হবে। এভাবে
আমরা f(n)
এর মান পাবো। কোন
সংখ্যার
ফ্যাক্টোরিয়ালের
লগারিদম এক থেকে
এক থেকে ঐ সংখ্যা
পর্যন্ত
সবগুলো
সংখ্যার
লগারিদম এর যোগফলের
সমান।
ln n! = ln 1 + ln 2 + ln 3 + … + ln n
অ্যালগোরিদম
বাস্তবায়ন
নিচের
গ্লোবাল
অ্যারেগুলো
ডিক্লেয়ার
করা যাক
#define MAX 100001
double lf[MAX], ans[MAX];
lf
অ্যারেটাতে lf[i] = lni! এর
মান রাখি।
res = lf[1] = 0.0;
for(res = 0, i = 2; i < MAX; i++)
{
res += log((double)i);
lf[i] = res;
}
ans অ্যারেটায়
ans[i] = f(i) এর
মান বের করে
রাখি। ans[n] হবে
উত্তর।
for(i = 2; i < MAX; i += 2)
{
res =
lf[i/2-1];
res = lf[i-2] - (i - 2) * log(2.0) - res - res;
// res = ln f(i)
ans[i] = exp(res);
}
scanf("%d",&n);
printf("%.4lf\n",ans[n]);