1209. Function with factorials

For the given even positive integer n find the value of

f(n) =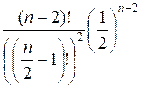

Input. Even positive integer n (1 £ n £ 100000).

Output. Print the value of f(n) with four digits after the decimal point.

Sample input	Sample output
4	0.5000

SOLUTION

mathematics

Algorithm analysis

Take the logarithm of equation f(n) = :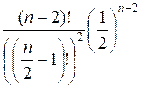

ln f(n) = ln(n – 2)! – –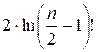

Calculate the right part of equation and apply the exponential function base e to it. You will get f(n). Logarithm of factorial can be computed as the sum of logarithms:

ln n! = ln 1 + ln 2 + ln 3 + … + ln n

Algorithm realization

Declare the global arrays.

#define MAX 100001

double lf[MAX], ans[MAX];

Fill the array lf, where lf[i] = lni!.

res = lf[1] = 0.0;

for(res = 0, i = 2; i < MAX; i++)

{

res += log((double)i);

lf[i] = res;

}

Fill the array ans, where ans[i] = f(i).

for(i = 2; i < MAX; i += 2)

{

res = lf[i/2-1];

res = lf[i-2] - (i - 2) * log(2.0) - res - res; // res = ln f(i)

ans[i] = exp(res);

}

scanf("%d",&n);

printf("%.4lf\n",ans[n]);

Java realization

import java.util.*;

import java.io.*;

public class Main

{

public static final int MAX = 100001;

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

PrintWriter out = new PrintWriter(System.out,true);

int i, n = con.nextInt();

double lf[] = new double[MAX],

ans[] = new double [MAX];

double res = lf[1] = 0.0;

for(res = 0, i = 2; i < MAX; i++)

{

res += Math.log(i);

lf[i] = res;

}

for(i = 2; i < MAX; i += 2)

{

res = lf[i/2-1];

res = lf[i-2] - (i - 2) * Math.log(2.0) - res - res;

ans[i] = Math.exp(res);

}

out.printf(Locale.US,"%.4f\n",ans[n]);

}

}