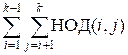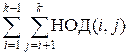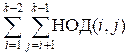1229. НОД Экстрим 2
По заданному числу
n вычислить значение G, где
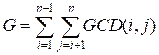
Через НОД(i, j)
обозначен наибольший общий делитель чисел i
и j.
Для тех, кто не встречался со
знаком суммирования объясняем, что значение
G формально по приведённой формуле вычисляется при помощи следующего кода:
g = 0;
for (i = 1; i < n; i++)
for (j = i + 1; j <= n; j++)
g += gcd(i,
j);
Вход. Состоит из не более чем 20000 строк. Каждая строка
содержит одно натуральное число n (1
< n ≤ 4 * 106). Последняя строка содержит n = 0 и не обрабатывается.
Выход. Для каждого
входного значения n в отдельной
строке вывести соответствующее значение G. Значение G помещается в 64-битовое
знаковое целое число.
|
Пример
входа |
Пример
выхода |
|
6 10 100 200000 0 |
20 67 13015 143295493160 |
РЕШЕНИЕ
теория
чисел – функция Эйлера
Анализ алгоритма
Пусть d[k] = 
.
Например d[2] =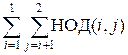 
= 
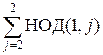= НОД(1, 2) = 1.
Можно заметить,
что d[k] = 
=
+ 
= d[k
– 1] +
Остается
показать, как вычислять значение 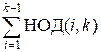быстрее
обыкновенного суммирования.
Лемма. Пусть n делится
на d и НОД(x, n) = d. Тогда x = dk для некоторого
натурального k. А из соотношения НОД(dk, n)
= d следует, что НОД(k, n/d) = 1.
Теорема. Обозначим через f(n) =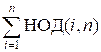 
. Тогда f(n) = 
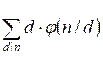для всех делителей d числа n. Через 
здесь обозначена
функция Эйлера.
Доказательство. Количество таких i, для которых НОД(i, n) = 1, равно 
. Количество таких i
(i ≤ n), для которых НОД(i, n) = d
(d делитель n, i = dk), равно количеству таких k (k ≤ n / d), для которых НОД(k, n/d) = 1, или 
. Значением НОД(i,
n) могут быть только делители числа n. Для нахождения f(n) остается
просуммировать значения 
по всем делителям d числа n.
Пример
Непосредственное
вычисление: f(6) =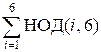 
=
НОД(1, 6) +
НОД(2, 6) + НОД(3, 6) + НОД(4, 6) + НОД(5, 6) + НОД(6, 6) =
1 + 2 + 3 + 2 +
1 + 6 = 15
Вычисление по
формуле:
f(6) =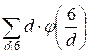 
= 
+ 
+ 
+ 
=
= 
+ 
+ 
+ 
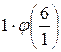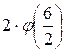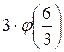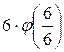= 2 + 4 + 3 + 6 = 15
И в первом, и во
втором случае 15 является суммой двух единиц (
), двух двоек (
), одной тройки (
) и одной шестерки (
).
Реализация алгоритма
Объявляем
массивы. fi[i] хранит значение
функции Эйлера j(i).
#define MAX 4000010
long long
d[MAX], fi[MAX];
Функция FillEuler заполняет массив fi так что fi[i] = j(i), i < MAX.
void FillEuler(void)
{
Изначально положим значение fi[i] равным i.
for(i = 1; i < MAX;
i++) fi[i] = i;
Каждое четное число i имеет простой делитель p = 2. Для ускорения работы функции
обработаем его отдельно. Для каждого четного i положим fi[i] = fi[i] * (1 – 1 / 2) = fi[i] / 2.
for(i = 2; i
< MAX; i+=2) fi[i] /= 2;
Перебираем все возможные нечетные
делители i = 3, 5, 7, … .
for(i = 3; i
< MAX; i+=2)
if(fi[i] ==
i)
Если fi[i] = i, то число i является простым. Число i является простым делителем для всякого j, представимого в виде k
* i для каждого натурального k.
for(j =
i; j < MAX; j += i)
Если i является простым делителем j,
то положим fi(j) = fi(j) * (1 – 1/i).
fi[j] -= fi[j]/i;
}
Перед вызовом функции f значения d[i] уже содержит j(i). Тело функции f добавляет в d[j] значения так, чтобы в конце работы
функции d[j] содержало 
согласно формуле,
приведенной в теореме.
void f(void)
{
int i,
SQRT_MAX = sqrt(1.0*MAX);
for(i = 2; i
<= SQRT_MAX; i++)
{
d[i*i] += i * fi[i];
Число i является делителем j.
Поэтому в d[j] следует прибавить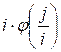 
. Поскольку делителем j также является число j / i,
то в d[j] следует добавить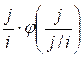 
= 
. Если i2 = j, то к
d[j] следует прибавлять не два
слагаемых, а только одно =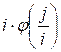 
.
// for(j = i * i +
i; j < MAX; j += i)
// d[j] += i * fi[j / i] + j / i * fi[i];
В реализации можно избежать
целочисленного деления. Для этого следует заметить, что поскольку значение
переменной j каждый раз увеличивается
на i, то значение j / i
будет увеличиваться в цикле на единицу. Положим изначально k = j / i = (i
* i + i) / i = i + 1 и далее при каждой итерации цикла
будем увеличивать k на 1.
for(j = i *
i + i, k = i + 1; j < MAX; j += i, k++)
d[j] += i * fi[k] + k * fi[i];
}
Цикл по i достаточно продолжать до 
, так как если i –
делитель j и i > , то с учетом того что j
/ i < можно утверждать, что
делитель i числа j был уже учтен когда рассматривался делитель j / i.
}
Основная часть программы. Инициализируем массивы. Положим d[i] = j(i).
memset(d,0,sizeof(d));
FillEuler();
memcpy(d,fi,sizeof(fi));
f();
for(i = 3; i < MAX; i++)
d[i] += d[i-1];
while(scanf("%lld",&n),n)
printf("%lld\n",d[n]);
import java.util.*;
public class Main
{
public final static int MAX = 4000001;
public static long d[] = new long[MAX];
public static int fi[] = new int[MAX];
static void FillEuler()
{
for(int i = 2; i < MAX; i++) fi[i] = i;
for(int i = 2; i < MAX; i+=2) fi[i] /= 2;
for(int i = 3; i < MAX; i+=2)
if(fi[i] == i)
for(int j = i; j < MAX; j += i) fi[j] -= fi[j]/i;
}
static void f()
{
int SQRT_MAX = (int)Math.sqrt(1.0*MAX);
for(int i = 2; i <= SQRT_MAX; i++)
{
d[i*i] += i * fi[i];
for(int j = i * i + i, k = i + 1; j < MAX; j += i, k++)
d[j] += i * fi[k] + k * fi[i];
}
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
FillEuler();
for(int i = 0; i < MAX; i++)
d[i] = fi[i];
f();
for(int i = 3; i < MAX; i++)
d[i] += d[i-1];
while(true)
{
int n = con.nextInt();
if (n == 0) break;
System.out.println(d[n]);
}
}
}