1229. GCD Extreme II

 

For a given number n calculate the value of G, where

G =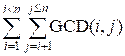

Here GCD(i, j) means the greatest common divisor of integers i and j.

 

For those who have trouble understanding summation notation, the meaning of G is given in the following code:

g = 0;

for (i = 1; i < n; i++)

for (j = i + 1; j <= n; j++)

  g += gcd(i, j);

 

Input. Consists of no more than 20000 lines. Each line contains an integer n (1 < n < 4 * 106). Input is terminated by a line containing a single zero and should not be processed.

 

Output. For each input number n print in a separate line the corresponding value of G. The value of G will fit in a 64-bit signed integer.

 

Sample input

Sample output

6

10

100            

200000

0

20

67

13015

143295493160

 

SOLUTION

number theory – Euler function

 

Algorithm analysis

Let d[k] = .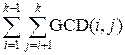

For example d[2] = 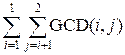 =  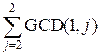= GCD(1, 2) = 1.

You can see that d[k] =  =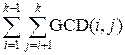

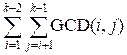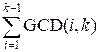 +  = d[k – 1]  +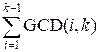

 

It remains to show how to calculate the value of 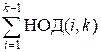 faster than usual summation.

 

Lema. Let n is divisible by d and GCD(x, n) = d. Then x = dk for some positive integer k. From the relation GCD(dk, n) = d it follows that GCD(k, n/d) = 1.

Theorem. Let f(n) = 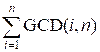. Then f(n) =  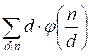for all divisors d of number n.  indicates here the Euler function.

Proof. The number of such i, for which GCD(i, n) = 1, equals to . The number of such i (i ≤ n), for which GCD(i, n) = d (d is a divisor of n, i = dk), equals to the number of such k (k ≤ n / d), for which GCD(k, n/d) = 1 or . The value of GCD(i, n) can be only the divisors of n. To find the value f(n) it remains to sum the values  over all divisors d of n.

 

Example

Consider the direct calculation: f(6) =  =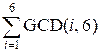

GCD(1, 6) + GCD(2, 6) + GCD(3, 6) + GCD(4, 6) + GCD(5, 6) + GCD(6, 6) =

1 + 2 + 3 + 2 + 1 + 6 = 15

Consider the calculation using the formula:

f(6) =  =  +  +  +  =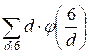

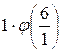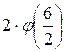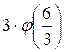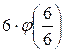=  +  +  +  = 2 + 4 + 3 + 6 = 15

In the first and in the second case 15 is the sum of two units (), two doules (), one triple () and one sextuple ().

 

Algorithm realization

Declare the arrays. fi[i] stores the value of the Euler function j(i).

 

#define MAX 4000010

long long d[MAX], fi[MAX];

 

The function FillEuler fills the array fi so that fi[i] = j(i), i < MAX.

 

void FillEuler(void)

{

 

Initially set the value of fi[i] equal to i.

 

  for(i = 1; i < MAX; i++) fi[i] = i;

 

Each even number i has a prime divisor p = 2. To speed up the function working time, process it separately. For each even number i set fi[i] = fi[i] * (1 – 1 / 2) = fi[i] / 2.

 

  for(i = 2; i < MAX; i+=2) fi[i] /= 2;

 

Enumerate all the possible odd divisors i = 3, 5, 7, … .

 

  for(i = 3; i < MAX; i+=2)

    if(fi[i] == i)

 

If fi[i] = i, then the number i is prime. The number i is a prime divisor for any j, represented in the form k * i for any positive integer k.

 

      for(j = i; j < MAX; j += i)

 

If i is a prime divisor of j, then set fi(j) = fi(j) * (1 – 1/i).

 

        fi[j] -= fi[j]/i;

}

 

Before calling the function f the values d[i] already contain j(i). The body of the function f adds to d[j] the values so that when the function finishes its work, the value d[j] contains  according to the formula given in the theorem.

 

void f(void)

{

 int i, SQRT_MAX = sqrt(1.0*MAX);

 for(i = 2; i <= SQRT_MAX; i++)

 {

   d[i*i] += i * fi[i];

 

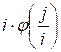The number i is a divisor of j. So we need to add to d[j] the value of . Since the number j has also a divisor j / i, add to d[j] the value of 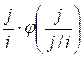 = . If i2 = j, add to d[j] not two terms, but only one  = .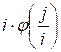

 

  // for(j = i * i + i; j < MAX; j += i)

  //   d[j] += i * fi[j / i] + j / i * fi[i];

 

We can avoid integer division in implementation. To do this note, that since the value of the variable j is incremented each time by i, then the value j / i will be increase by one in a loop. Set initially k = j / i = (i * i + i) / i = i + 1 and then increase k by 1 in each iteration.

 

   for(j = i * i + i, k = i + 1; j < MAX; j += i, k++)

     d[j] += i * fi[k] + k * fi[i];  

 

 }

 

Its sufficiently to continue the loop by i till , because if i is a divisor of j and i > , then considering the fact that j / i <  we can state that the divisor i of the number j was taken in account when we considered the divider j / i.

 

}

 

The main part of the program. Initialize the arrays. Let d[i] = j(i).

 

memset(d,0,sizeof(d));

FillEuler();

memcpy(d,fi,sizeof(fi));

 

 

f();

 

 

for(i = 3; i < MAX; i++)

  d[i] += d[i-1];

 

 

while(scanf("%lld",&n),n)

  printf("%lld\n",d[n]);

 

Java realization

 

import java.util.*;

 

public class Main

{

  public final static int MAX = 4000001;   

  public static long d[] = new long[MAX];

  public static int fi[] = new int[MAX];   

 

  static void FillEuler()

  {

    for(int i = 2; i < MAX; i++) fi[i] = i;

    for(int i = 2; i < MAX; i+=2) fi[i] /= 2;

 

    for(int i = 3; i < MAX; i+=2)

      if(fi[i] == i)

        for(int j = i; j < MAX; j += i) fi[j] -= fi[j]/i;

  }

 

  static void f()

  {

   int SQRT_MAX = (int)Math.sqrt(1.0*MAX);

   for(int i = 2; i <= SQRT_MAX; i++)

   {

     d[i*i] += i * fi[i];

     for(int j = i * i + i, k = i + 1; j < MAX; j += i, k++)

       d[j] += i * fi[k] + k * fi[i];  

   }

  }

 

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);  

    FillEuler();

    for(int i = 0; i < MAX; i++)

      d[i] = fi[i];

    f();

    for(int i = 3; i < MAX; i++)

      d[i] += d[i-1];

 

    while(true)

    {

      int n = con.nextInt();

      if (n == 0) break;

      System.out.println(d[n]);

    }

  }

}