1316. Equal balls

Ship grove. 1898. When comparing the color scheme of Ship Grove, one of Shishkin's later works, with that of his earlier paintings, it becomes clear that the landscape artist, like his contemporary genre painters, transitioned from a localized understanding of color to a restrained yet cohesive color palette. This palette is based on the depiction of light and shadow, which unifies the composition.

In this painting, Shishkin discovered a new tonal approach to color through the harmonious blending of the grayish-brown spruce trunks and the green moss in the foreground.

The painting is also notable for its innovative way of conveying the forest’s depth. The trees are not depicted in their entirety but are seemingly cut off by the frame. The spruces appear in close proximity to the viewer, yet when one looks at them, it is impossible to take in the entire painting at once.

In an opaque, closed box with a small hole in the top, there are n balls (n is an even number), half of which are black and the other half are white. You have a fair coin, which you begin flipping.

· If heads comes up, you remove a white ball;

· If tails comes up, you remove a black ball;

This process continues until exactly two balls remain in the urn. At this point, they will be of the same color, making further coin flips unnecessary. Up until this moment, the urn always contains at least one black and one white ball.

What is the probability that the described situation will occur?

Input. Each line represents a separate test case and contains one even integer n (0 < n £ 10⁵) – the number of balls in the box.

Output. For each test case, print the probability of the described situation occurring. The answer should be printed with eight decimal places.

Sample input	Sample output
6 10 256	0.62500000 0.72656250 0.94998552

SOLUTION

probability

Algorithm analysis

Let’s compute the probability of the opposite event X – that the last two balls removed are of different colors. For this to happen, exactly half of the first n – 2 removed balls must be white, and the other half must be black.

Consider a Bernoulli trial scheme, where the probability of success (e.g., drawing a white ball) is p = 1/2, and the probability of failure is q = 1 – p = 1/2. The probability that exactly (n – 2) / 2 of the first n – 2 removed balls are white is given by the formula:

P(X) = =

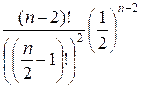
It remains to compute the value of P(X) for each input n and print 1 – P(X).

Although P(X) lies within the range [0, 1], its direct computation may lead to numerical issues. To avoid this, compute its logarithm:

ln P(X) = ln(n – 2)! – –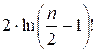

After computing the right-hand side of the equation, exponentiate the result to obtain P(X). The logarithm of a factorial is computed as the sum of logarithms:

ln n! = ln 1 + ln 2 + ln 3 + … + ln n

Since the program processes multiple test cases, all results should be precomputed and stored in an array.

Example

For n = 6 , the probability that the last two balls removed will be of different colors is

= =

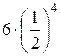The probability that the last two balls removed will be of the same color is

1 – = = 0,625

Algorithm implementation

Declare the necessary arrays. In the cell ans[i], store the value .

#define MAX 100001

double lf[MAX], ans[MAX];

Fill the array lf, where lf[i] stores the value ln i!.

res = lf[1] = 0.0;

for (res = 0, i = 2; i < MAX; i++)

{

res += log((double)i);

lf[i] = res;

}

For each value of i, compute and store the result in ans[i].

for (i = 2; i < MAX; i += 2)

{

res = lf[i/2-1];

res = lf[i-2] - (i - 2) * log(2.0) – res - res;

ans[i] = exp(res);

}

For each input value of n, compute and print the result.

while (scanf("%d",&n) == 1)

printf("%.8lf\n",1 - ans[n]);