1352. Сумма простых чисел

Вася полюбил простые числа. Он решил найти такую сумму первых n простых чисел, которая делится нацело на число k. Помогите ему в этом.

Вход. Одно целое число k (1 ≤ k ≤ 1000).

Выход. Выведите наименьшее возможное значение n.

Пример входа	Пример выхода
7	5

РЕШЕНИЕ

простые числа

Анализ алгоритма

Перебираем последовательность простых чисел (2, 3, 5, 7, …) и накапливаем их сумму. Как только эта сумма станет делиться на число k без остатка, выводим количество использованных слагаемых.

Пример

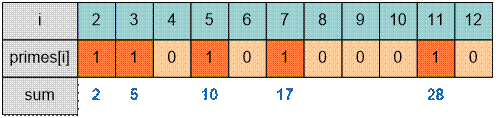
Сумма первых пяти простых чисел 2 + 3 + 5 + 7 + 11 равна 28 и делится на 7.

Реализация алгоритма

Функция prime возвращает 1, если число n является простым.

int prime(int n)

{

if (n == 2) return 1;

if (n % 2 == 0) return 0;

for(int i = 3; i <= sqrt(n); i += 2)

if(n % i == 0) return 0;

return 1;

}

Основная часть программы. Читаем значение k.

scanf("%d",&k);

В переменной s накапливается сумма простых чисел, а в переменной c – их количество.

s = c = 0;

Перебираем числа, начиная с 2. Если текущее число простое, прибавляем его к s и увеличиваем c. Как только сумма s становится кратной k, выполнение цикла останавливается.

for(i = 2;; i++)

{

if (prime(i))

{

s += i; c++;

if (s % k == 0) break;

}

}

Выводим минимальное количество первых простых чисел, сумма которых делится на k.

printf("%d\n",c);

Java реализация

import java.util.*;

public class Main

{

public static boolean prime(int n)

{

if (n == 2) return true;

if (n % 2 == 0) return false;

for(int i = 3; i <= Math.sqrt(n); i += 2)

if(n % i == 0) return false;

return true;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int k = con.nextInt();

int s = 0, c = 0;

for(int i = 2;; i++)

{

if (prime(i))

{

s += i; c++;

if (s % k == 0) break;

}

}

System.out.println(c);

con.close();

}

}

Python реализация

Функция prime возвращает 1, если число n является простым.

def prime(n):

if n == 2: return True

if n % 2 == 0: return False

for i in range(3, int(math.sqrt(n))+1, 2):

if n % i == 0: return False

return True

Основная часть программы. Читаем значение k.

k = int(input())

В переменной s накапливается сумма простых чисел, а в переменной c – их количество.

s = c = 0

i = 2

Перебираем числа, начиная с 2. Если текущее число простое, прибавляем его к s и увеличиваем c. Как только сумма s становится кратной k, выполнение цикла останавливается.

while True:

if (prime(i)):

s += i

c += 1

if s % k == 0: break

i += 1

Выводим минимальное количество первых простых чисел, сумма которых делится на k.

print(c);