1352. The sum of primes

Vasya fell in love with prime numbers. He decided to find such a sum of the first n prime numbers that is divisible by k. Help him with this task.

Input. One integer k (1 ≤ k ≤ 1000).

Output. Print the smallest possible value of n.

Sample input	Sample output
7	5

SOLUTION

prime numbers

Algorithm analysis

Iterate through the sequence of prime numbers (2, 3, 5, 7, …) and accumulate their sum. As soon as this sum becomes divisible by k without a remainder, print the number of terms used.

Example

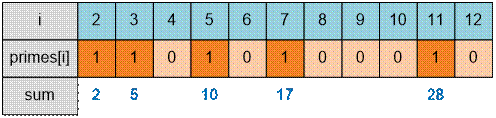
The sum of the first five prime numbers 2 + 3 + 5 + 7 + 11 equals 28 and is divisible by 7.

Algorithm implementation

The function prime returns 1 if the number n is prime.

int prime(int n)

{

if (n == 2) return 1;

if (n % 2 == 0) return 0;

for(int i = 3; i <= sqrt(n); i += 2)

if(n % i == 0) return 0;

return 1;

}

The main part of the program. Read the value of k.

scanf("%d",&k);

The variable s stores the sum of prime numbers, and the variable c stores their count.

s = c = 0;

Iterate over numbers starting from 2. If the current number is prime, add it to s and increase c. As soon as the sum s becomes divisible by k, the loop stops.

for(i = 2;; i++)

{

if (prime(i))

{

s += i; c++;

if (s % k == 0) break;

}

}

Print the minimum number of initial prime numbers whose sum is divisible by k.

printf("%d\n",c);

Java implementation

import java.util.*;

public class Main

{

public static boolean prime(int n)

{

if (n == 2) return true;

if (n % 2 == 0) return false;

for(int i = 3; i <= Math.sqrt(n); i += 2)

if(n % i == 0) return false;

return true;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int k = con.nextInt();

int s = 0, c = 0;

for(int i = 2;; i++)

{

if (prime(i))

{

s += i; c++;

if (s % k == 0) break;

}

}

System.out.println(c);

con.close();

}

}

Python implementation

The function prime returns 1 if the number n is prime.

def prime(n):

if n == 2: return True

if n % 2 == 0: return False

for i in range(3, int(math.sqrt(n))+1, 2):

if n % i == 0: return False

return True

The main part of the program. Read the value of k.

k = int(input())

The variable s stores the sum of prime numbers, and the variable c stores their count.

s = c = 0

i = 2

Iterate over numbers starting from 2. If the current number is prime, add it to s and increase c. As soon as the sum s becomes divisible by k, the loop stops.

while True:

if (prime(i)):

s += i

c += 1

if s % k == 0: break

i += 1

Print the minimum number of initial prime numbers whose sum is divisible by k.

print(c);