1409. Закон Джунглей

Акела – большой серый волк-одиночка, благодаря своей силе и хитрости стал вожаком стаи. Двенадцать лет Одинокий Волк водил стаю на охоту и с охоты, и за всё это время никто, ни один волк не попался в ловушку.

Акела постарел, стал слабее, и теперь хромой тигр Шерхан подружился с младшими волками стаи и те часто бегали за ним; Акела не допустил бы до этого, если бы прежняя сила дала ему возможность как следует проявлять свою власть.

С годами стал Акела подзабывать и Закон Джунглей. Нет, он не мог его нарушить, ибо Закон Джунглей уже давно стал частью его инстинктов, кроме того, он точно помнил контрольную сумму Закона.

И вот, молодые оппозиционные волки вместе с Шерханом, решили внести поправки и дополнения в этот Закон, так сказать расширить и дополнить. Можно только догадываться зачем им это понадобилось, и так как, к счастью, поправки были отклонены самим Хатхи, Джунгли могут спать спокойно.

Но все-таки интересно, как же мог выглядеть основной Закон с поправками и дополнениями оппозиционных волков, если известно, что его контрольная сумма при этом не изменилась.

Вход. Натуральное число n (1 ≤ n ≤ 10¹⁰⁰) – Закон Джунглей.

Выход. Вывести самое маленькое натуральное число m > n с такой же контрольной суммой (суммой цифр), как и у числа n – Закон Джунглей в редакции оппозиционных волков во главе с Шерханом.

Пример входа

77

Пример выхода

86

РЕШЕНИЕ

математика - экстремум

Анализ алгоритма

Найдем самую правую (последнюю) ненулевую цифру и уменьшим ее на 1. Далее слева от нее найдем цифру, которую можно увеличить на 1 (то есть не девятку). Все цифры, находящиеся за той, которую увеличили на 1, отсортируем по возрастанию. Так получим искомое наименьшее число с такой же контрольной суммой, как и исходное.

Пример

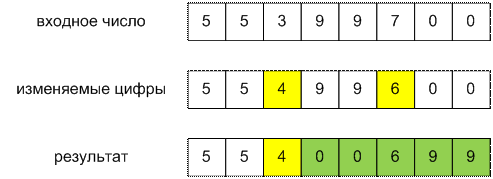
Реализация алгоритма

Объявим символьный массив, в котором будем хранить входное число.

char s[200];

Считываем входное число в массив s, начиная с первой (не нулевой) позиции. Вычисляем длину строки len.

s[0] = '0'; gets(s+1); len = strlen(s); cur = len - 1;

Ищем первую с конца ненулевую цифру.

while(s[cur] == '0') cur--;

Уменьшаем ее на 1.

s[cur--]--;

Ищем слева от уменьшенной цифры такую, которую можно увеличить на 1. То есть пропускаем все девятки.

while(s[cur] == '9') cur--;

Увеличиваем цифру на 1.

s[cur]++;

Сортируем цифры.

sort(s+cur+1,s+len);

Выводим результат. Если в нулевой позиции (ведущим) стоит ноль, то не выводим его.

puts(s + (s[0] == '0'));