1417. Ход ферзя

На шахматной доске размером m × n стоит ферзь. Определите, сколько клеток находятся под его боем.

Вход. Четыре натуральных числа: размеры доски m и n, а также координаты ферзя x и y (1 ≤ x ≤ m ≤ 10⁹, 1 ≤ y ≤ n ≤ 10⁹).

Выход. Выведите количество клеток, находящихся под боем ферзя.

Пример входа	Пример выхода
8 8 4 5	27

РЕШЕНИЕ

математика

Анализ алгоритма

Ферзь – это шахматная фигура, которая ходит (и бьет) по горизонтали, вертикали и диагонали.

Строка, в которой стоит ферзь, содержит n клеток. Поэтому количество клеток, доступных для горизонтального хода, равно n – 1. Аналогично, столбец, в котором находится ферзь, содержит m клеток, следовательно, число клеток, доступных для вертикального хода, равно m – 1.

Таким образом, под боем ферзя по горизонтали и вертикали находятся n – 1 + m – 1 клеток.

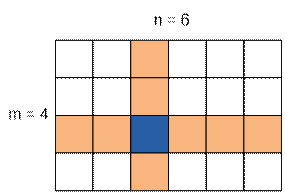
Разделим доску на четыре области, проведя через клетку с ферзем горизонтальную и вертикальную линии. В каждой из этих областей подсчитаем количество клеток, находящихся под его ударом.

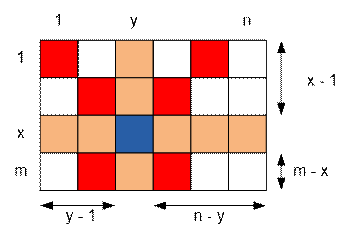
Рассмотрим например правую верхнюю четверть. Ее длина составляет n – y клеток, а ширина x – 1 клеток. Следовательно, количество клеток под боем ферзя в этой области равно min(x – 1, n – y).

Аналогично:

· в левой верхней четверти под боем окажется min(x – 1, y – 1) клеток;

· в левой нижней четверти под боем окажется min(m – x, y – 1) клеток;

· в правой нижней четверти под боем окажется min(m – x, n – y) клеток;

Пример

Рассмотрим пример, в котором размер доски равен 8 × 8, а ферзь находится в позиции (4, 5).

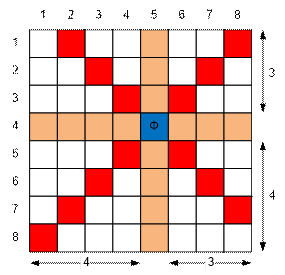
Под горизонтальным и вертикальным ударом ферзя находится n – 1 + m – 1 = 7 + 7 = 14 клеток. Теперь рассмотрим четыре четверти, в каждой из которых подсчитаем количество клеток под его боем:

· в левой верхней четверти min(4, 3) = 3 клетки;

· в левой нижней четверти min(4, 4) = 4 клетки;

· в правой нижней четверти min(3, 4) = 3 клетки;

· в правой верхней четверти min(3, 3) = 3 клетки;

Всего под боем ферзя находится 14 + 3 + 4 + 3 + 3 = 27 клеток.

Реализация алгоритма

Читаем входные данные.

scanf("%d %d %d %d", &m, &n, &x, &y);

Сохраняем в переменную s количество клеток, находящихся под боем ферзя при горизонтальных и вертикальных ходах.

s = m - 1 + n - 1; // horiz & vertical

Затем добавляем клетки, которые ферзь бьет по диагоналям.

s += min(m - x, n - y); // (x,y) = (m, n)

s += min(m - x, y - 1); // (x,y) = (m, 1)

s += min(x - 1, n - y); // (x,y) = (1, n)

s += min(x - 1, y - 1); // (x,y) = (1, 1)

Выводим ответ.

printf("%lld\n",s);