1417. Queen Move

A queen is placed on an m × n chessboard. Determine how many squares are under its attack.

Input. Four positive integers: the size of the chessboard m and n, as well as the coordinates of the queen x and y (1 ≤ x ≤ m ≤ 10⁹, 1 ≤ y ≤ n ≤ 10⁹).

Output. Print the number of squares under the queen’s attack.

Sample input	Sample output
8 8 4 5	27

SOLUTION

mathematics

Algorithm analysis

The queen is a chess piece that moves (and attacks) horizontally, vertically, and diagonally.

The row where the queen is placed contains n squares, so the number of squares available for horizontal movement is n – 1. Similarly, the column where the queen is located contains m squares, meaning the number of squares available for vertical movement is m – 1.

Thus, the number of squares under the queen’s attack horizontally and vertically is n – 1 + m – 1.

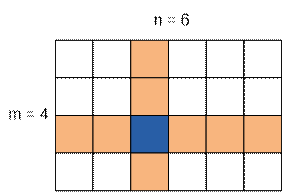
Divide the board into four areas by drawing horizontal and vertical lines through the square where the queen is located. In each of these areas, count the number of squares under her attack.

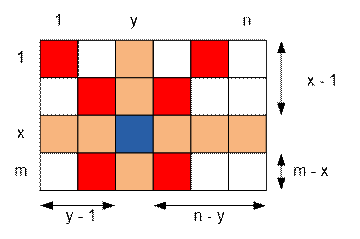
Consider, for example, the upper-right quadrant. Its length is n – y squares, and its width is x – 1 squares. Therefore, the number of squares under the queen’s attack in this area is min(x – 1, n – y).

Similarly:

· In the upper-left quadrant, there are min(x – 1, y – 1) squares;

· In the lower-left quadrant, there are min(m – x, y – 1) squares;

· In the lower-right quadrant, there are min(m – x, n – y) squares;

Example

Consider the example where the board size is 8 × 8 and the queen is located at position (4, 5).

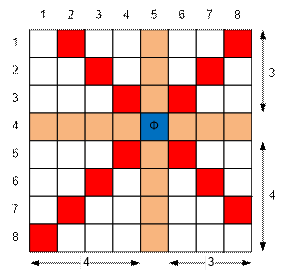
The number of squares under the queen’s horizontal and vertical attack is n – 1 + m – 1 = 7 + 7 = 14. Now, let’s consider the four quadrants, in each of which we’ll count the number of squares under its attack:

· in the upper left quadrant there are min(4, 3) = 3 squares;

· in the lower left quadrant there are min(4, 4) = 4 squares;

· in the lower right quadrant there are min(3, 4) = 3 squares;

· in the upper right quarter there are min(3, 3) = 3 squares;

Thus, the total number of squares under the queen’s attack is

14 + 3 + 4 + 3 + 3 = 27

Algorithm implementation

Read the input data.

scanf("%d %d %d %d", &m, &n, &x, &y);

Store in the variable s the number of squares under the queen’s attack from horizontal and vertical moves.

s = m - 1 + n - 1; // horiz & vertical

Then, add the squares that the queen attacks along the diagonals.

s += min(m - x, n - y); // (x,y) -> (m, n)

s += min(m - x, y - 1); // (x,y) -> (m, 1)

s += min(x - 1, n - y); // (x,y) -> (1, n)

s += min(x - 1, y - 1); // (x,y) -> (1, 1)

Print the answer.

printf("%lld\n", s);