1421. Сближение
кораблей
31 августа
1986 года, 22.00.
Теплый южный вечер,
небо в звездах,
море спокойное. Пароход
"Адмирал Нахимов" с пассажирами на борту отошел от причала порта
Новороссийск и последовал к выходу из Цемесской бухты, направляясь в Сочи.
Пройдя Пенайские банки, пароход лег на курс 160 градусов, следуя 12-узловым
ходом. На борту его находилось 1234 человека: 888 пассажиров, 346 членов
экипажа…
В это
время грузовой теплоход-сухогруз "Петр
Васев" входил в
Цемесскую бухту, следуя со
скоростью 11,5 узлов курсом 36 градусов. На борту судна было около 30 тысяч
тонн ячменя из Канады. Суда сближались на пересекавшихся курсах …
В свой последний
рейс паром «Донья Пас» вышел 20
декабря 1987 года. Около 22 часов того
же дня в районе
острова Мариндуке паром
столкнулся с танкером
«Вектор» (Vertor). От удара «Донья Пас» разломилась пополам. 8000
баррелей нефти с танкера воспламенилось, начался пожар…
В 1910 году в
Гренландии многотонная глыба льда оторвалась от материка и начала свое плаванье
в водах северной
Атлантики. Годом раньше
на верфях судостроительной компании «Харланд энд Вольф» в Куинс-Айленд (Белфаст, Северная Ирландия)
был заложен крупнейший океанский лайнер типа «Олимпик», который в дальнейшем
был назван «Титаник». Во время первого рейса
14 апреля 1912 года он столкнулся с тем самым айсбергом и через 2 часа
40 минут затонул. На борту находилось 1 316 пассажиров и 892 члена экипажа,
всего 2 208 человек. Из них спаслось 706 человек, погибло свыше 1 500…
Можно привести
ещё много примеров
этой печальной статистики.
Тем более, что столкновения происходят не только на
воде, но и в воздухе. Как правило, во всех перечисленных выше случаях причиной
катастроф являлся человеческий фактор, другими словами, ошибки
людей. Поэтому оценка возможности столкновения двух объектов, движущихся
пересекающимися курсами, должна быть автоматизирована.
Решим несколько
упрощенную задачу. Два объекта равномерно прямолинейно движутся из точек А и В
соответственно в заданных направлениях с заданными скоростями v1 и v2. Определите наименьшее расстояние, на котором могут
оказаться эти объекты.
Вход. В первой строке четыре целых числа – координаты точек А и
В в метрах (x1 y1 x2 y2),
все координаты в диапазоне от -100 до 100 (включительно). Во второй строке –
два целых числа: курс первого объекта в градусах (от 0 до 359) и его скорость v1 в метрах в секунду (от 1
до 10). В третьей строке – два целых числа: курс второго объекта в градусах (от
0 до 359) и его скорость v2
в метрах в секунду (от 1 до 10). Все
числа в строках отделяются друг от друга
хотя бы одним пробелом.
Выход. В выходной строке выведите одно число – наименьшее
расстояние, на котором могут оказаться эти объекты, в формате с двумя знаками
после запятой.
|
Пример
входа |
Пример
выхода |
|
0 0 2 0 45 2 135 1 |
0.63 |
РЕШЕНИЕ
математика
- экстремум
Анализ алгоритма
Первый корабль
стартует из точки А(x1, y1) со скоростью v1 и курсом α, а второй
стартует из точки B(x2, y2) со скоростью v2 и курсом β. Обозначим
через (x1(t), y1(t)
координаты первого корабля через t
секунд и через (x2(t), y2(t) соответственно координаты второго.
Тогда
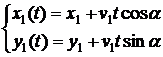 ,
, 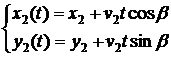
Расстояние между
кораблями в момент времени t равно
dist(t) = ![]() =
=
![]()
Для нахождения
кратчайшего расстояния между кораблями следует найти минимум функции dist(t), где t ≥ 0. Найдем минимум функции dist2(t), приравняв ее производную к нулю.
![]() +
+
![]() = 0,
= 0,
![]() +
+ ![]() = 0,
= 0,
![]() =
=
![]() +
+ ![]() ,
,
![]() =
= ![]() +
+ ![]() ,
,
откуда и
находится искомое значение t.
Траектория движения кораблей – прямые линии. Если кратчайшее
расстояние между кораблями достигается в случае их движения в обратном
направлении (при t < 0), то это
означает, что при их реальном движении они расходятся – то есть с каждой
секундой расстояние между ними увеличивается. В этом случае кратчайшее
расстояние между кораблями достигается на старте, то есть при t = 0.
Реализация алгоритма
Функция dist
возвращает расстояние между кораблями в момент времени t.
double dist(double t)
{
double res = sqr(xx2 - xx1 + t *(v2 * cos(beta) - v1
* cos(alpha))) +
sqr(yy2 - yy1 + t *(v2 *
sin(beta) - v1 * sin(alpha)));
return sqrt(res);
}
Основная часть программы.
scanf("%lf
%lf %lf %lf",&xx1,&yy1,&xx2,&yy2);
scanf("%lf
%lf %lf %lf",&alpha,&v1,&beta,&v2);
Переведем углы в радианную меру.
alpha = alpha * PI / 180.0; beta = beta
* PI / 180.0;
Находим t, при
котором достигается минимум функции dist(t).
t = (xx1 - xx2) * (v2 * cos(beta) - v1 *
cos(alpha)) +
(yy1 - yy2) * (v2 * sin(beta) - v1 * sin(alpha));
temp = (v1*v1 + v2*v2 - 2 * v1 * v2 *
cos(alpha - beta));
Значение temp
близко к нулю, если корабли движутся параллельно. Кратчайшее расстояние между
ними можно положить равным расстоянию в точке t = 0.
if (fabs(temp) < EPS) res = dist(0);
else
{
t /= temp;
if (t < 0) t = 0;
res = dist(t);
}
printf("%.2lf\n",res);