1453. Форд-Беллман
Дан
ориентированный граф, в котором допускаются кратные рёбра и петли. Каждое ребро
имеет целочисленный вес (в том числе отрицательный). Гарантируется, что в графе
нет циклов отрицательного веса.
Найдите длины
кратчайших путей от вершины с номером 1 до всех остальных вершин графа.
Вход. В первой строке заданы два числа:
количество вершин графа n (1 ≤ n ≤ 100) и количество рёбер m (0 ≤ m ≤ 10000).
Далее следуют m троек чисел, описывающих рёбра:
начало ребра, конец ребра и его вес. Вес задаётся целым числом в диапазоне от -100 до 100.
Выход. Выведите n чисел – кратчайшие расстояния
от вершины с номером 1 до каждой вершины графа.
Если путь до
некоторой вершины отсутствует, вместо длины пути выведите число 30000.
|
Пример
входа |
Пример
выхода |
|
4 5 1 2 10 2 3 10 1 3 100 3 1 -10 2 3 1 |
0 10 11
30000 |
РЕШЕНИЕ
графы –
алгоритм Беллмана-Форда
Анализ алгоритма
Поскольку ребра графа могут содержать отрицательные веса, для
решения задачи достаточно использовать алгоритм Беллмана – Форда.
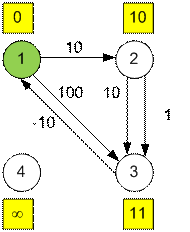
Пример
Граф из примера имеет
следующий вид:
Реализация алгоритма
Объявим
константы.
#define MAX 10002
#define INF 0x3F3F3F3F
Объявим рабочие
массивы:
· Ребро графа (x[i], y[i])
весом w[i] хранится в виде
тройки (x[i],
y[i], w[i]).
·
d[i] – это кратчайшее найденное на данный момент
расстояние от стартовой вершины (у нас это вершина 1) до вершины i.
int x[MAX], y[MAX], w[MAX], d[MAX];
Функция Bellman_Ford реализует
алгоритм Беллмана – Форда.
void Bellman_Ford(void)
{
memset(d,0x3F,sizeof(d));
d[1] = 0;
for (int i = 1; i
<= n; i++) // for stage = 1, 2, ..., n
for (int j = 1; j
<= m; j++) // for each edge try to relax it
if (d[x[j]] < INF)
if (d[y[j]] > d[x[j]] + w[j])
d[y[j]] = d[x[j]] + w[j];
}
Основная часть программы. Читаем входные данные.
scanf("%d
%d",&n,&m);
for (i = 1; i <= m; i++)
scanf("%d %d %d",&x[i],&y[i],&w[i]);
Вызываем
алгоритм Беллмана – Форда.
Bellman_Ford();
Если d[i] осталось равным INF, значит пути из вершины 1 в вершину i
не существует. В таком случае вместо INF следует вывести число 30000, как
указано в условии задачи.
for (i = 1; i <= n; i++)
if (d[i] == INF) d[i] = 30000;
Выводим ответ – кратчайшие
расстояния от вершины 1 до всех остальных вершин графа.
for (i = 1; i < n; i++)
printf("%d ",d[i]);
printf("%d\n",d[n]);
Реализация алгоритма – класс
Объявим
константу плюс бесконечность.
#define INF 0x3F3F3F3F
Объявим класс Edge, содержащий
номера вершин From и To, которые оно соединяет, а также его длину
Len.
class Edge
{
public:
int From, To, Len;
Edge(int From, int
To, int Len) : From(From), To(To), Len(Len) {}
};
Объявим класс Graph. Он содержит
количество вершин графа n, а также список рёбер g, задающих структуру
графа.
class Graph
{
public:
int n;
vector<Edge> g;
Graph(int n = 1) : n(n)
{
g.clear();
}
Функция AddEdge добавляет в граф ориентированное ребро (From, To)
длины Len.
void AddEdge(int
From, int To, int
Len)
{
g.push_back(Edge(From,To,Len));
}
Функция Bellman_Ford запускает алгоритм Беллмана -
Форда из вершины Source. Вторым аргументом передается массив кратчайших
расстояний d.
void Bellman_Ford(int Source, vector<int>
&d)
{
int stage, i;
Инициализируем все элементы массива d значением плюс
бесконечность.
d.assign(n+1,INF); d[Source] = 0;
Выполняем n фаз алгоритма Беллмана – Форда, то есть релаксацию всех рёбер.
for(stage = 0; stage < n; stage++)
На каждой фазе последовательно проходим по списку рёбер и выполняем их
релаксацию.
for (i = 0; i < g.size(); i++)
{
Edge e = g[i];
if (d[e.From] < INF)
if (d[e.To] > d[e.From] + e.Len)
d[e.To] = d[e.From] + e.Len;
}
}
};
Объявим массив
кратчайших расстояний dist. Объявим указатель на граф g.
vector<int>
dist;
Graph *g;
Основная часть
программы. Читаем входные данные. Граф g храним как список ребер.
scanf("%d
%d",&n,&m);
g = new
Graph(n);
for(i = 1; i <= m; i++)
{
scanf("%d %d %d",&From,&To,&Len);
g->AddEdge(From,To,Len);
}
Запускаем алгоритм Беллмана - Форда из вершины 1.
g->Bellman_Ford(1,dist);
Если путь до вершины i отсутствует, то присваиваем dist[i] =
INF.
for(i = 1; i <= n; i++)
if (dist[i] == INF) dist[i] = 30000;
Выводим
кратчайшие расстояния от вершины 1 до всех остальных вершин.
for(i = 1; i < n; i++)
printf("%d ",dist[i]);
printf("%d\n",dist[n]);
Реализация алгоритма – Shortest Path Faster Algorithm
input G,v
for each u ∈ V(G)
let dist[u] = ∞
let dist[v] = 0
let Q be an
initially empty queue
push(Q,v)
while not
empty(Q)
let u = pop(Q)
for each (u,w) ∈ E(G)
if dist[w] > dist[u] + weight(u,w)
dist[w] = dist[u] + weight(u,w)
if w is not in Q
push(Q,w)
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
#define INF 0x3F3F3F3F
using namespace std;
int k, i, n, m, x, y, w;
struct Edge
{
public:
int To, Len;
Edge(int To, int
Len) : To(To), Len(Len) {}
};
vector<vector<Edge> > g;
int *dist;
// Shortest Path Faster
Algorithm
void Bellman_Ford(int start,
vector<vector<Edge> > &g, int
*dist)
{
int *used = new int[n+1];
memset(used,0,sizeof(int)*(n+1));
queue<int> q;
q.push(start);
memset(dist,0x3F,sizeof(int)*(n+1));
dist[start] = 0; used[start] = 1;
while(!q.empty())
{
int u = q.front(); q.pop();
used[u] = 0; // remove u from queue
for(int
i = 0; i < g[u].size(); i++)
{
int to = g[u][i].To;
int w = g[u][i].Len;
// relax all edges (u, to) adjacent to u
if (dist[to] > dist[u] + w)
{
dist[to] = dist[u] + w;
if(!used[to]) //
if to is not in queue
{
q.push(to);
used[to] = 1;
}
}
}
}
delete[] used;
}
int main(void)
{
scanf("%d %d",&n,&m);
g.resize(n+1);
dist = new int[n+1];
for(i = 0; i < m; i++)
{
scanf("%d %d %d",&x,&y,&w);
g[x].push_back(Edge(y,w));
}
Bellman_Ford(1,g,dist);
for(i = 1; i <= n; i++)
if (dist[i] == INF) dist[i] = 30000;
for(i = 1; i < n; i++)
printf("%d ",dist[i]);
printf("%d\n",dist[n]);
delete[] dist;
return 0;
}