1501. Конусное расстояние

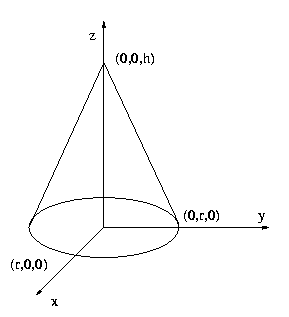
В трехмерном пространстве задан конус так, что его основание с радиусом r и центром в точке (0, 0, 0) лежит в плоскости z = 0. Вершина конуса расположена в точке (0, 0, h). На его поверхности заданы две точки в конусных координатах. Конусной координатой точки p называется пара чисел (d, A), где d – расстояние от вершины конуса до точки p, а A (A < 360) – угол в градусах между плоскостью y = 0 и плоскостью, проходящей через точки (0,0,0), (0, 0, h) и p, считая против часовой стрелки от направления оси x.

 На поверхности конуса заданы две точки p₁ = (d₁, A₁) и p₂ = (d₂, A₂). Найти кратчайшее расстояние между p₁ и p₂, измеряемое по поверхности конуса.

Вход. Каждая строка содержит 6 действительных чисел: r, h, d₁, A₁, d₂, A₂.

Выход. Для каждого теста вывести наименьшее расстояние между точками p₁ и p₂ с двумя десятичными знаками.

Пример входа

3.0 4.0 2.0 0.0 4.0 0.0
3.0 4.0 2.0 90.0 4.0 0.0
6.0 8.0 2.14 75.2 9.58 114.3
3.0 4.0 5.0 0.0 5.0 90.0
 

Пример выхода

2.00
3.26
7.66
4.54

РЕШЕНИЕ

геометрия

Анализ алгоритма

Переведем меру углов из градусной в радианную. Поскольку в 180 градусах содержится p радиан, то x градусам соответствует x * p / 180 радиан. Изобразим развертку конуса, разрезав его по прямой AB₁, которая проходит через вершину A(0, 0, h) и точку p₁. Поскольку ищется минимальное расстояние между точками p₁ и p₂, то развертку отобразим той стороной, для которой Ðp₁Ap₂ £ ½ÐB₁AB₂ (равенство достигается когда абсолютное значение разности A₂ – A₁ равно p). Обозначим j = Ðp₁Ap₂. Поскольку длина образующей конуса l равна AB₁ = , а длина дуги B₁B₂ развертки равна 2pr, то | B₁B₂ | = AB₁ * ÐB₁AB₂ или 2pr = l * ÐB₁AB₂. Здесь использована формула длины дуги , где l – длина дуги, r – радиус окружности, a – величина угла в радианах.

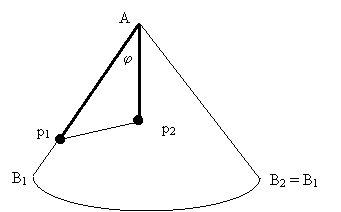
Обозначим через dA минимальное расстояние между углами A₁ и A₂. В развертке углу B₁AB₂ соответствует 2p радиан, а углу j соответствует dA радиан. Имеем пропорцию:

Откуда j = ÐB₁AB₂ * dA / 2p = (2pr / l) * dA / 2p = r * dA / l. Поскольку длины Ap₁ и Ap₂ известны, то из треугольника p₁Ap₂ по теореме косинусов находим длину отрезка p₁p₂. Она равна .

Реализация алгоритма

Объявим константу p:

const double MY_PI = acos(-1.0);

Читаем входные данные, переводим меру углов из градусной в радианную. Вычисляем минимальное угловое расстояние da между p₁ и p₂.

while (scanf("%lf %lf %lf %lf %lf %lf",&r, &h, &d1, &a1, &d2, &a2) == 6)

{

a1 *= MY_PI / 180; a2 *= MY_PI / 180;

da = fabs(a2 - a1);

if (da > MY_PI) da = 2*MY_PI - da;

Вычисляем длину образующей l и угол j, на который отображается угол dA на развертке. По теореме косинусов находим расстояние между точками p₁ и p₂ и выводим результат.

l = sqrt(r*r+h*h);

fi = da * r / l;

l = sqrt(d1*d1 + d2*d2 - 2*d1*d2*cos(fi));

printf("%.2lf\n",l);

}