1503. Circum triangle
You are given n distinct points on
the boundary of a circle with radius r whose center is at the origin. As
the points are on the same circle no three of them are collinear, so any three
of them creates a valid triangle. Your job is to find the summation of areas of
these triangles.
Input. Contains at most 16 tests. Each test starts with two
integers n (0 £ n £ 500) and
r (0 < r £ 100).
Here n is the number of points and r is the radius of the circle.
You can assume that the center of the circle is always at the origin. This line
is followed by n lines each of which contains a floating-point number θ (0.0
≤ θ < 360.00) which denotes the angle
in degree the designated point creates with respect to the origin with x-axis.
So, for example if θ is 30.00 degree then the Cartesian coordinate of
the intended point is (r×cos(30.00°), r×sin(30.00°)).
The last line contains n = r = 0 and is not
processed.
Output. For each test case print one line. This line contains
an integer which is the total area (rounded to the nearest integer) of all
possible triangles formed by the given n points.
|
Sample
input |
Sample output |
|
5 10 10.00 100.00 300.00 310.00 320.00 3 20 10.00 100.00 300.00 0 0 |
286 320 |
SOLUTION
geometry + full search
Algorithm analysis
Consider
triangle ABC. We calculate its area as the area of the circle minus the area of
the three black segments, as shown in the figure.
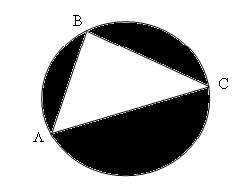
Thus, the
desired area is equal to 
minus the total
area of the segments, which, as will be shown below, can be calculated in O(n2)
time.
Recall that the
area of the sector of radius r subtracted by angle a is equal to 
. The area of the corresponding segment is equal to the area
of the sector minus the area of an isosceles triangle with lateral side r
and vertex angle a. Thus, the area of the segment is
Ssegment = 
= 
Initially, we
set the desired area of all triangles equal to res = = 
. After that, we will sequentially subtract the areas
of the segments from res.
Consider a
segment connecting the points Pi and Pj (i < j). In the variable s, we calculate the area of the segment
that we pass when moving along a circle from the point Pi to Pj counterclockwise (in the direction of increasing angles).
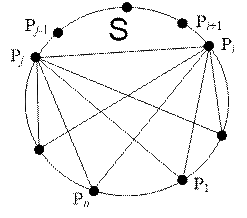
The area s
of a segment is subtracted
from the total area res as many times as there are points between Pi and Pj from the side of the segment of area 
r2 – s. The area s of a segment is subtracted when
calculating the areas of triangles PiPjPk, where k runs through the points located from Pj to Pi while moving counterclockwise (k
takes the values j + 1, j + 2, …, i – 2, i – 1). There will be pnts1
= n – (j – i + 1) such points.
Subtract from res pnts1 times
the area s.
Accordingly, from the side of the segment of
area s will be pnts2 = n – pnts1 – 2 points. This number of times we must subtract the area r2 – s of the segment
from res.
Algorithm realization
Find the degree
measure of points, convert it to radian and put it into array d (d[i] contains the
radian measure of the i - th point).
double d[MAX];
Read the input data till the end of the file.
while(scanf("%d
%d",&n,&r), n + r)
{
Store the radian measure of points into array d.
for(i = 0; i
< n; i++)
{
scanf("%lf",&d[i]);
d[i] = d[i] * PI / 180;
}
Sort an array d in ascending order.
sort(d,d + n);
Initially store in the variable res the area of 
circles
of radius r, that is the
value = 
. Assign to the variable r2 the value
of 
, and sq is the area of one circle 
.
res = n * (n - 1) * (n - 2) / 6 * PI * r * r;
r2 = r * r / 2.0; sq = PI * r * r;
Iterate through all pairs of points using two indices i and j.
for(i = 0; i
< n; i++)
for(j = i +
1; j < n; j++)
{
Find the angle alfa between the
points i and j, that equals
to d[j] – d[i]. If alfa is less than 
, then when moving from i to j we pass through
a smaller segment and its area is equal to 
. Otherwise, when moving from i to j, we pass
through a larger segment, and in this case its area is equal to 
, where 
.
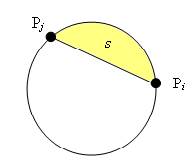
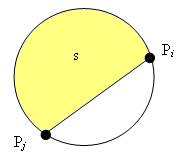
In both cases, the variable s
is assigned the area of the segment that we pass when moving from Pi to Pj
counterclockwise.
alfa = d[j] - d[i];
if (alfa
< PI)
s = r2 * (alfa - sin(alfa));
else
{
alfa = 2 * PI - alfa,
s = sq - r2 * (alfa - sin(alfa));
}
The number of points points lying on a segment whose area is 
equal to n
– (j – i + 1). Thus, points times the area of segment s must
be subtracted from the value of res.
points = n - (j - i + 1);
res -= s * points;
The number of points lying on the segment
of area s is equal to points = n – points – 2. The area
of the opposite segment is equal to sq
– s. It remains to subtract it from res
points times.
points = n - points - 2;
res -= (sq - s) * points;
}
Print the required area res.
printf("%.0lf\n",res);
}