1504. Максимальный четырехугольник

В четырехугольнике, в который вписана окружность, известны длины двух соседних сторон и его периметр. Вычислить максимально возможное значение радиуса окружности.

Вход. Первая строка содержит количество тестов n (n £ 100). Каждая следующая строка содержит три целых числа p, a, b, где a и b – длины соседних сторон, а p – периметр четырехугольника.

Выход. Для каждого теста вместе с его номером вывести в отдельной строке максимально возможное значение радиуса окружности с шестью точками после десятичной точки. Если такой окружности не существует, то вывести фразу Eta Shombhob Na., которая в переводе с языка Бангла обозначает «это не возможно».

Пример входа	Пример выхода
2 20 5 6 20 10 12	Case 1: 2.449490 Case 2: Eta Shombhob Na.

РЕШЕНИЕ

геометрия

Анализ алгоритма

Обозначим через c и d длины двух других сторон. Поскольку в четырехугольник вписана окружность, то a + c = b + d. Учитывая, что a + b + c + d = p, получим a + c = b + d = p / 2. Откуда c = p / 2 – a, d = p / 2 – b. Если длины сторон c и d будут не положительными, то искомого четырехугольника не существует.

Площадь четырехугольника выражается через периметр и радиус вписанной окружности по формуле: s = (p/2) * r. Радиус вписанной окружности будет максимальным, если будет максимальной площадь четырехугольника. Площадь четырехугольника выражается через длины его сторон a, b, c, d и противоположные углы B и D по формуле:

s =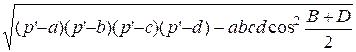, где p’= p/2 – полупериметр.

Распишем первый множитель: p' – a = = . Учитывая соотношение a + c = b + d, последнее выражение равно = с. Аналогично p' – b = = = = d, p' – c = a, p' – d = b. Формулу площади четырехугольника таким образом можно переписать в виде s =.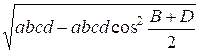

Площадь s будет максимальной, если abcd cos² = 0, то есть при B + D = 180°. Сумма противоположных углов равна 180°, следовательно четырехугольник с заданными длинами сторон будет иметь максимальную площадь, если он вписан в окружность.

Искомая максимальная площадь равна s = .

Пример

Для первого теста длины двух других сторон равны c = 5, d = 4. Они положительны, следовательно четырехугольник с заданными характеристиками существует и его площадь s равна = 24.49490. Радиус вписанной окружности равен r = 2 * s / p = 2.449490.

Для второго теста сумма двух сторон больше периметра, значит такого четырехугольника не существует.

Реализация алгоритма

Для каждого теста читаем входные данные, вычисляем длины двух других сторон c и d.

scanf("%lf %lf %lf",&p,&a,&b);

c = p / 2 - a; d = p / 2 - b;

Если четырехугольник со сторонами a, b, c, d существует (их длины положительны), то вычисляем радиус вписанной окружности и выводим результат. Иначе выводим сообщение о невозможности построения четырехугольника.

if (c > 0 && d > 0)

{

s = sqrt(a * b * c * d);

r = 2 * s / p;

printf("Case %d: %.6lf\n",i+1,r);

}

else printf("Case %d: Eta Shombhob Na.\n", i+1);