1506. Пересекающиеся лестницы

Вдоль узкой улицы расположены два дома – один слева, другой справа.

Лестница длиной x футов установлена у основания правого дома и опирается на дом, находящийся слева.Другая лестница длиной y футов стоит у основания левого дома и опирается на правый дом. Лестницы пересекаются на высоте  футов от земли. Необходимо найти ширину улицы.

Вход. Каждая строка представляет отдельный тест и содержит три положительных вещественных числа: x, y и c.

Выход. Для каждого теста выведите в отдельной строке одно вещественное число – ширину улицы, с точностью до трёх десятичных знаков.

Пример входа	Пример выхода
30 40 10 12.619429 8.163332 3 10 10 3 10 10 1	26.033 7.000 8.000 9.798

РЕШЕНИЕ

геометрия - бинарный поиск

Анализ алгоритма

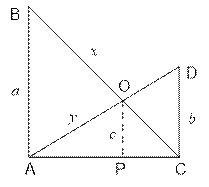
Треугольники AOP и ADC подобны: .

Треугольники COP и CBA подобны: .

Откуда

,

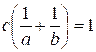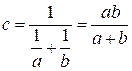
Будем искать ширину улицы d = AC методом бинарного поиска.

Изначально положим 0 ≤ d ≤ min(x, y). Зная значения d, x и y, можно вычислить a, b и c. При фиксированных x и y с увеличением d величина c уменьшается.

Реализация алгоритма

Читаем входные данные для каждого теста.

while(scanf("%lf %lf %lf",&x,&y,&c) == 3)

{

Установим значения: left = 0, right = min(x,y). Далее в процессе выполнения цикла всегда выполняется неравенство left ≤ d ≤ right.

left = 0;

if (x < y) right = x; else right = y;

d = (left + right) / 2;

do

{

Вычисляем значения a, b, c.

a = sqrt(x*x - d*d); b = sqrt(y*y - d*d);

c1 = 1/(1/a + 1/b);

Если вычисленное значение c1 меньше заданного с, необходимо уменьшить верхнюю границу d. В противном случае следует увеличить нижнюю границу.

if (c1 < c) right = (left + right) / 2;

else left = (left + right) / 2;

d = (left + right) / 2;

Вычисления выполняются до достижения требуемой в условии задачи точности – четырёх десятичных знаков.

} while (fabs(c1 - c) > 0.00001);

Выводим результат.

printf("%.3lf\n",d);

}

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

con.useLocale(new Locale("US"));

while(con.hasNext())

{

double x = con.nextDouble();

double y = con.nextDouble();

double c = con.nextDouble();

double Left = 0, Right, a, b, c1;

if (x < y) Right = x; else Right = y;

double d = (Left + Right) / 2;

do

{

a = Math.sqrt(x*x - d*d);

b = Math.sqrt(y*y - d*d);

c1 = 1/(1/a + 1/b);

if (c1 < c) Right = (Left + Right) / 2;

else Left = (Left + Right) / 2;

d = (Left + Right) / 2;

} while (Math.abs(c1 - c) > 0.00001);

System.out.format(Locale.US,"%.3f\n",d);

}

}

}