1506. Crossed ladders

Along a narrow street, there are two houses – one on the left and the other on the right.

A ladder of length x feet is placed at the base of the right house and leans against the house on the left. Another ladder of length y feet stands at the base of the left house and leans against the right house. The ladders cross at a height of  feet above the ground. Find the width of the street.

Input. Each line represents a separate test case and contains three positive real numbers: x, y and c.

Output. For each test case, print one real number – the width of the street, rounded to three decimal places.

Sampe input	Sample output
30 40 10 12.619429 8.163332 3 10 10 3 10 10 1	26.033 7.000 8.000 9.798

SOLUTION

geometry – binary search

Algorithm analysis

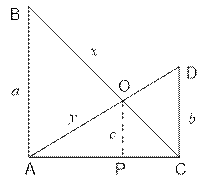
The tiangles AOP and ADC are similar: .

The triangles COP and CBA are also similar: .

Whence

, .

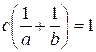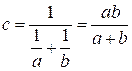We’ll find the width of the street d = AC using the binary search method.

Initially, let 0 ≤ d ≤ min(x, y). Given the values of d, x and y, we can compute a, b and c. For fixed x and y, as d increases, the value of c decreases.

Algorithm implementation

Read the input data for each test case.

while(scanf("%lf %lf %lf",&x,&y,&c) == 3)

{

Set the initial values: left = 0, right = min(x,y). During the execution of the loop, the inequality left ≤ d ≤ right always holds.

left = 0;

if (x < y) right = x; else right = y;

d = (left + right) / 2;

do

{

Compute the values of a, b, c.

a = sqrt(x*x - d*d); b = sqrt(y*y - d*d);

c1 = 1/(1/a + 1/b);

If the computed value c1 is less than the given c, the upper bound of d should be decreased. Otherwise, the lower bound should be increased.

if (c1 < c) right = (left + right) / 2;

else left = (left + right) / 2;

d = (left + right) / 2;

The computations are performed until the required accuracy specified in the problem statement is reached – four decimal places.

} while (fabs(c1 - c) > 0.00001);

Print the answer.

printf("%.3lf\n",d);

}

Java implementation

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

con.useLocale(new Locale("US"));

while(con.hasNext())

{

double x = con.nextDouble();

double y = con.nextDouble();

double c = con.nextDouble();

double Left = 0, Right, a, b, c1;

if (x < y) Right = x; else Right = y;

double d = (Left + Right) / 2;

do

{

a = Math.sqrt(x*x - d*d);

b = Math.sqrt(y*y - d*d);

c1 = 1/(1/a + 1/b);

if (c1 < c) Right = (Left + Right) / 2;

else Left = (Left + Right) / 2;

d = (Left + Right) / 2;

} while (Math.abs(c1 - c) > 0.00001);

System.out.format(Locale.US,"%.3f\n",d);

}

}

}