1510. Окружность
через три точки
На плоскости
заданы три точки, не лежащие на одной прямой. Найдите уравнение окружности,
проходящей через них. Решение выведите в виде
(x – a)2
+ (y – b)2 = r2
(1)
и
x2 + y2 + cx + dy + e = 0 (2)
Вход. Каждая строка содержит шесть
действительных чисел Ax, Ay, Bx, By,
Cx, Cy – координаты трех точек A(Ax, Ay),
B(Bx, By), C(Cx, Cy).
Выход. Для
каждого теста необходимо вывести уравнение окружности в двух форматах как
показано в примере. Значения h, k, r,
c, d и e в уравнениях 1 и 2
необходимо выводить с тремя десятичными знаками. Если некоторое из значений h, k,
c, d, e равно нулю, то
соответствующее слагаемое выводить не следует. Знаки плюс и минус следует
выводить по необходимости – так, чтобы избегать нескольких знаков перед числом.
Знаки сложения, вычитания и равенства следует разделять от ближайших символов
одним пробелом с каждой стороны. Никаких других лишних пробелов выводить не
следует. После каждой пары уравнений следует выводить пустую строку. Формат
вывода приведен в примере.
|
Пример входа |
|
7.0
-5.0 -1.0 1.0 0.0 -6.0 1.0
7.0 8.0 6.0 7.0 -2.0 |
|
|
|
Пример выхода |
|
(x -
3.000)^2 + (y + 2.000)^2 = 5.000^2 x^2 +
y^2 - 6.000x + 4.000y - 12.000 = 0 (x -
3.921)^2 + (y - 2.447)^2 = 5.409^2 x^2 +
y^2 - 7.842x - 4.895y - 7.895 = 0 |
РЕШЕНИЕ
геометрия
Анализ алгоритма
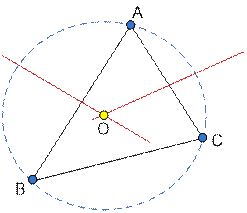
Построим
серединные перпендикуляры к отрезкам AB и AC. Точка их пересечения и будет
центром искомой окружности О. Радиус окружности равен расстоянию OA.
Реализация
алгоритма
Определим константу
EPS:
#define EPS 1e-6
Функция kramer решает систему линейных
уравнений
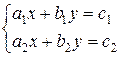
методом Крамера
d =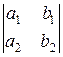 
, dx = 
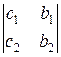, dy = 
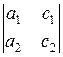, x = 
, y = 
, d ¹ 0
и возвращает:
·
0, если система
имеет единственное решение;
·
1, если система
не имеет решений (прямые параллельны и не совпадают);
·
2, если система имеет
бесконечное количество решений (прямые совпадают);
int
kramer(double a1, double
b1, double c1,
double
a2, double b2, double
c2, double &x, double
&y)
{
double d = a1
* b2 - a2 * b1;
double dx =
c1 * b2 - c2 * b1;
double dy =
a1 * c2 - a2 * c1;
if (!d) return (dx == 0.0) + 1;
x = dx/d; y = dy/d;
return 0;
}
Функция midperpend по заданным координатам концов отрезка A(x1, y1)
и B(x2, y2) строит серединный
перпендикуляр ax + by + c
= 0. Поскольку вектора AB(x2
– x1, y2 – y1)
и (a, b) коллинеарны, то
a = x2 – x1, b = y2 – y1
Серединный перпендикуляр проходит через точку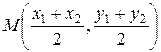 
– середину отрезка АВ,
значит
ax + by + c = (x2
– x1) 
+ (y2 – y1) 
+ c = 0,
откуда
c =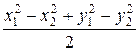 
void
midperpend(double x1, double
y1, double x2, double
y2,
double
&a, double &b,
double &c)
{
a = x2 - x1;
b = y2 - y1;
c = (x1*x1 - x2*x2 + y1*y1 - y2*y2) / 2;
}
Функция circle по трем точкам A(x1, y1), В(x2,
y2) и С(x3, y3) находит центр окружности (xc, yc) и радиус r, который через них проходит. Для этого
строятся серединные перпендикуляры к отрезкам AB и AC, после чего находится
точка их пересечения О – центр искомой окружности. Радиус r
вычисляется как расстояние между точками O и A.
void
circle(double x1, double
y1, double x2, double
y2, double x3,
double
y3, double &xc, double
&yc, double &r)
{
double
a1,b1,c1,a2,b2,c2;
midperpend(x1,y1,x2,y2,a1,b1,c1);
midperpend(x1,y1,x3,y3,a2,b2,c2);
kramer(a1,b1,-c1,a2,b2,-c2,xc,yc);
r = sqrt((x1 - xc)*(x1 - xc) + (y1 - yc)*(y1
- yc));
}
Основная часть
программы. Читаем входные данные.
while(scanf("%lf %lf %lf %lf %lf %lf",
&x_1,&y_1,&x_2,&y_2,&x_3,&y_3)
== 6)
{
Для каждого теста находим центр (xc,
yc) и радиус r окружности,
проходящей через три точки.
circle(x_1,y_1,x_2,y_2,x_3,y_3,xc,yc,r);
Выводим уравнение окружности в формате (x – a)2
+ (y – b)2 = r2.
if (fabs(xc)
< EPS) printf("x^2"); else
{
printf("(x");
if (xc
>= 0.0) printf(" - "); else printf(" + ");
printf("%.3lf)^2",fabs(xc));
}
printf(" +
");
if (fabs(yc)
< EPS) printf("y^2"); else
{
printf("(y");
if (yc
>= 0.0) printf(" - "); else printf(" +
");
printf("%.3lf)^2",fabs(yc));
}
printf(" =
%.3lf^2\n",r);
Выводим уравнение окружности в виде x2 + y2
+ cx + dy + e = 0.
printf("x^2 +
y^2");
if (fabs(xc)
> EPS)
{
if (xc >
0.0) printf(" - "); else printf(" +
");
printf("%.3lfx",2*fabs(xc));
}
if (fabs(yc)
> EPS)
{
if (yc >
0.0) printf(" - "); else printf(" +
");
printf("%.3lfy",2*fabs(yc));
}
r1 = xc*xc + yc*yc - r*r;
if (fabs(r1)
> EPS)
{
if (r1 >
0.0) printf(" + "); else printf(" -
");
printf("%.3lf",fabs(r1));
}
printf(" =
0\n\n");
}