1510. Circle through three points
Three points are given on
the plane that do not lie on one line. Find the equation of the circle that
passes through them. Print the solution in the form
(x – a)2 + (y – b)2
= r2 (1)
and
x2 + y2 + cx + dy + e = 0 (2)
Input. Each line contains six real
numbers Ax, Ay, Bx, By, Cx,
Cy – the
coordinates of three points A(Ax, Ay), B(Bx,
By), C(Cx, Cy).
Output. For each test case print the
equation of a circle in two formats as given in a sample. The values of h, k,
r, c, d and e in Equations 1 and 2 are to be
printed with three decimal digits. If some of h, k, c, d,
e is zero, do not print the
corresponding term. Plus and minus signs in the equations should be changed as
needed to avoid multiple signs before a number. Plus, minus, and equal signs
must be separated from the adjacent characters by a single space on each side.
No other spaces are to appear in the equations. Print a single blank line after
each equation pair. See output format in example.
|
Sample input |
|
7.0
-5.0 -1.0 1.0 0.0 -6.0 1.0
7.0 8.0 6.0 7.0 -2.0 |
|
|
|
Sample output |
|
(x -
3.000)^2 + (y + 2.000)^2 = 5.000^2 x^2 +
y^2 - 6.000x + 4.000y - 12.000 = 0 (x -
3.921)^2 + (y - 2.447)^2 = 5.409^2 x^2 +
y^2 - 7.842x - 4.895y - 7.895 = 0 |
SOLUTION
geometry
Algorithm analysis
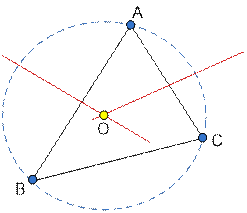
Construct the middle point perpendiculars
to the segments AB and AC. The point of their intersection will be the center
of the desired circle O. The radius of the circle is equal to the distance OA.
Algorithm realization
Define the constant EPS:
#define EPS 1e-6
Function kramer solves the system of linear equations
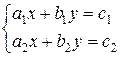
using the Cramer’s method
d = 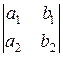 , dx =
, dx = 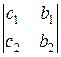 , dy =
, dy = 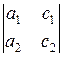 , x =
, x = ![]() , y =
, y = ![]() , d ¹ 0
, d ¹ 0
and returns:
·
0, if the system
has a unique solution;
·
1, if the system
has no solutions (lines are parallel and do not coincide);
·
2, if the system
has an infinite number of solutions (lines coincide);
int
kramer(double a1, double
b1, double c1,
double a2,
double b2, double
c2, double &x, double
&y)
{
double d = a1
* b2 - a2 * b1;
double dx =
c1 * b2 - c2 * b1;
double dy =
a1 * c2 - a2 * c1;
if (!d) return (dx == 0.0) + 1;
x = dx/d; y = dy/d;
return 0;
}
Function midperpend using the
coordinates of the ends of segment A(x1, y1) and B(x2, y2) constructs the midpoint perpendicular ax + by + c = 0. Since the vectors AB(x2 – x1, y2 – y1)
and (a, b) are
collinear, then
a = x2 – x1, b = y2 – y1
The midpoint perpendicular passes through the point 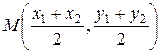 – the middle of
segment ÀÂ, so
– the middle of
segment ÀÂ, so
ax + by + c = (x2
– x1) ![]() + (y2 – y1)
+ (y2 – y1) ![]() + c = 0,
+ c = 0,
wherefrom
c = 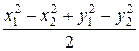
void
midperpend(double x1, double
y1, double x2, double
y2,
double
&a, double &b,
double &c)
{
a = x2 - x1;
b = y2 - y1;
c = (x1*x1 - x2*x2 + y1*y1 - y2*y2) / 2;
}
The function circle uses three points A(x1, y1), Â(x2, y2)
and Ñ(x3, y3) to find the center of the circle (xc, yc) and the radius r that passes
through them. For this, the perpendiculars
to the segments AB and AC are constructed, after which the point of their
intersection O is found – the center of the desired circle. The radius r is calculated as the distance between points O and A.
void
circle(double x1, double
y1, double x2, double
y2, double x3,
double
y3, double &xc, double
&yc, double &r)
{
double
a1,b1,c1,a2,b2,c2;
midperpend(x1,y1,x2,y2,a1,b1,c1);
midperpend(x1,y1,x3,y3,a2,b2,c2);
kramer(a1,b1,-c1,a2,b2,-c2,xc,yc);
r = sqrt((x1 - xc)*(x1 - xc) + (y1 - yc)*(y1
- yc));
}
The main part of
the program. Read the
input data.
while(scanf("%lf %lf %lf %lf %lf %lf",
&x_1,&y_1,&x_2,&y_2,&x_3,&y_3)
== 6)
{
For each test find the center (xc,
yc) and the radius r of the
circle that pass
through three points.
circle(x_1,y_1,x_2,y_2,x_3,y_3,xc,yc,r);
Print
the equation of a circle in the form (x –
a)2 + (y – b)2
= r2.
if (fabs(xc)
< EPS) printf("x^2"); else
{
printf("(x");
if (xc
>= 0.0) printf(" - "); else printf(" +
");
printf("%.3lf)^2",fabs(xc));
}
printf(" +
");
if (fabs(yc)
< EPS) printf("y^2"); else
{
printf("(y");
if (yc
>= 0.0) printf(" - "); else printf(" +
");
printf("%.3lf)^2",fabs(yc));
}
printf(" =
%.3lf^2\n",r);
Print
the equation of a circle in the form x2 + y2
+ cx + dy + e = 0.
printf("x^2 +
y^2");
if (fabs(xc)
> EPS)
{
if (xc >
0.0) printf(" - "); else printf(" +
");
printf("%.3lfx",2*fabs(xc));
}
if (fabs(yc)
> EPS)
{
if (yc >
0.0) printf(" - "); else printf(" +
");
printf("%.3lfy",2*fabs(yc));
}
r1 = xc*xc + yc*yc - r*r;
if (fabs(r1)
> EPS)
{
if (r1 >
0.0) printf(" + "); else printf(" -
");
printf("%.3lf",fabs(r1));
}
printf(" =
0\n\n");
}