1511. Cake Division
You have a rectangular cake of a given
length and width, and want to divide it into a certain number of equal-area
rectangular pieces. Each cut you make must be parallel to the sides of the
cake, and must completely cut one of the existing pieces into two parts.
(Therefore, cutting the cake into n
pieces will require exactly n – 1
cuts.)
You prefer square pieces to those with a
larger aspect ratio. (Here, we define the “aspect ratio” of a piece to be the
length of its longer side divided by the length of its shorter side.) You
should cut the cake in such a way as to minimize the maximum aspect ratio of
all the resulting pieces.
For
example, if the cake is 2x3, and you want to cut it into six pieces, you can
cut it into six 1x1 pieces. Each piece has an aspect ratio of 1.0, which is the
smallest possible aspect ratio. Therefore, this solution is optimal.
One way to cut a 5x5 cake into 5 pieces is
to first cut it into two pieces of sizes 2x5 and 3x5. Cut the smaller of these
two in half (each of size 2 x 5/2) and the larger in thirds (each of size 3 x
5/3). The largest aspect ratio of these five pieces is 3/(5/3) = 1.8. There is
no way to cut this cake into 5 equal-area pieces that all have an aspect ratio
of less than 1.8.
Input. Three integers: length and width of a
cake, and the number of rectangular pieces
you must divide the cake. It is known that 1 ≤ length, width ≤
1000, 1 ≤ pieces ≤ 10.
Output. Cut
the cake to minimize the maximum aspect ratio of all the resulting pieces.
Print this aspect ratio with 4 digits after the decimal point.
Sample
input
2
3 6
5
5 5
950
430 9
Sample
output
1.0000
1.8000
1.2573
SOLUTION
recursion + full search
Algorithm
analysis
Благодаря верхнему ограничению на число
кусков pieces, задача может быть
просто решена полным перебором разрезаний торта. Если кусок размером length на width следует разбить на pieces
кусков, то после совершения первого разреза (который по условию задачи можно совершить
либо по горизонтали, либо по вертикали) площади двух полученных кусков должны
быть пропорциональны числам 1 и pieces
– 1, или 2 и pieces – 2 и так далее.
То есть после первого разреза должны получаться два куска размером i * length
/ pieces на width и ((pieces – i ) * length / pieces на width, или length на i * width / pieces и length на (pieces – i) * width / pieces, где 1 £ i < pieces. При этом дальше первый кусок следует делить на i кусков, а второй на pieces – i кусков.
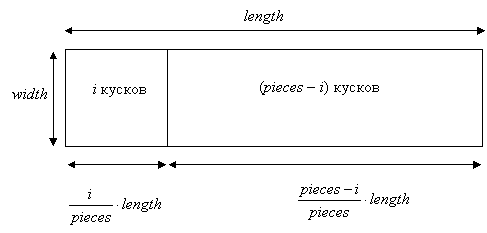
Совершаем разрез исходного куска на две
части и далее рекурсивно запускаем разрезание каждой из полученных частей. Ищем
такое разрезание, при котором максимум отношения кусков является наименьшим.
Algorithm
realization
Функция cut возвращает наименьшее возможное максимальное значение
отношения сторон полученных pieces кусков в результате разрезания
прямоугольника длины length и ширины width.
double cut(double length, double width, int
pieces)
{
double temp, res = 1e100;
int i;
Если pieces равно
1, то возвращаем отношение сторон текущего куска.
if (pieces == 1) return max(length,width) / min(length,width);
Совершаем вертикальный разрез торта на две части, каждая из
которых дальше будет делиться на i и pieces – i кусков.
for(i = 1; i < pieces; i++)
{
temp = max(cut(i * length / pieces,width,i),
cut((pieces - i) * length /
pieces,width,pieces - i));
if (temp < res) res = temp;
}
Совершаем горизонтальный разрез торта на две части, каждая из
которых дальше будет делиться на i и pieces – i кусков.
for(i = 1; i < pieces; i++)
{
temp = max(cut(length,i * width / pieces,i),
cut(length,(pieces - i) * width
/ pieces,pieces - i));
if (temp < res) res = temp;
}
return res;
}
Основной цикл
программы.
while(scanf("%d %d %d",&length,
&width, &pieces) == 3)
{
double res = cut(length,width,pieces);;
printf("%.4lf\n",res);
}
Временная оценка работы алгоритма
Пусть f(pieces) – функция, которая возвращает количество вызовов функции cut в зависимости от значения pieces.
Очевидно,
что f(1) = 1, так как в этом случае сразу после вызова функции выйдем по
команде return.
При pieces = 2 первый вызов функции cut будет
со значением pieces = 2. Далее кусок будем стараться разделить
пополам вертикальным разрезом, в результате чего дважды будет вызвана f(1).
Потом попробуем совершить горизонтальный разрез, снова будет дважды вызвана
f(1). Итого получим f(2) = 5 вызовов функции cut.
Пусть pieces = 3. Первый вертикальный разрез разобьет кусок на две части, первый из
которых далее надо будет делить на 1 часть, а второй на 2 части. Второй
вертикальный разрез также разобьет кусок на две части, первый из которых далее
надо будет делить на 2 части, а второй на 1 часть. Аналогичное количество
вызовов функции следует произвести при горизонтальных разрезах. Итого
f(3) = 1 + 2 * ( (f(1) + f(2) ) + (f(2) + f(1)) ) = 1 + 2 * 2 * (1 + 5) = 25
В общем
случае f(n) = 1 + ![]() = 1 +
= 1 + ![]() .
.
Например:
f(4) = 1 + ![]() = 1 + 4 * (1 + 5 + 25)
= 125,
= 1 + 4 * (1 + 5 + 25)
= 125,
f(5) = 1 + ![]() = 1 + 4 * (1 + 5 + 25
+ 125) = 625
= 1 + 4 * (1 + 5 + 25
+ 125) = 625
Докажем методом математической индукции, что f(n) = 5n-1.
База
индукции. f(1) = 50
= 1.
Шаг
индукции. f(n)
= 1 + ![]() = 1 + 4 (50
+ 51 + … + 5n-2)
= 1 +
= 1 + 4 (50
+ 51 + … + 5n-2)
= 1 + ![]() = 5n-1.
= 5n-1.
Временная
оценка работы программы составляет O(5pieces).