1512. Последовательность Фарея
Дробь h / k
называется правильной, если она лежит между 0 и 1, а h и k не имеют общего
делителя кроме 1. Для любого натурального числа n ≥ 1, последовательностью Фарея порядка n называется последовательность Fn
всех правильных дробей, знаменатели которых не превосходят n вместе с "дробью" 1/1, упорядоченных по возрастанию.
Например, последовательность F5
имеет вид:
![]()
По заданному n необходимо найти k-ую
дробь в последовательности Fn.
Вход. Состоит из нескольких строк, каждая из
которых содержит два натуральных числа n
и k, 1 ≤ n ≤ 1000, k
достаточно мало чтобы существовал k-ый
элемент в Fn. (Длина Fn приблизительно равна
0.3039635n2).
Выход. Для каждой
входной пары чисел в отдельной строке вывести k-ый элемент Fn
в формате, указанном в примере.
|
Пример
входа |
Пример
выхода |
|
5 5 5 1 5 9 5 10 117 348 288 10000 |
1/2 1/5 4/5 1/1 9/109 78/197 |
РЕШЕНИЕ
рекурсия
Анализ алгоритма
Последовательность
Фарея n-го порядка можно задать
следующим образом:
Fn = 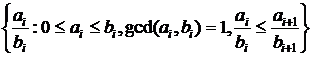
Дробь 0 / n считаем нулевым элементом в Fn.
Последовательность
Фарея порядка n + 1 можно построить
из последовательности порядка n по
следующему правилу:
·
Копируем все элементы последовательности порядка n.
·
Если сумма знаменателей в двух соседних дробях последовательности
порядка n дает число не большее, чем n + 1, то вставляем между этими дробями
их медианту, равную отношению суммы их числителей к сумме знаменателей.
Начиная с F1
= {0/1, 1/1}, будем рекурсивно строить F2, F3, …, Fn. То есть брать две соседние
дроби a / b и c / d и записывать между ними медианту (a + c)
/ (b + d), если b + d ≤ n. Рекурсивно сгенерируем все элементы Fn вплоть до k-го,
который и выведем.
Последовательность
Фарея порядка n содержит все элементы
последовательности Фарея порядка n –
1, а также все несократимые дроби со знаменателями, равными n. Последних имеется в точности φ(n). Обозначив через Ln длину последовательности Fn, получим рекуррентное соотношение: Ln = Ln-1 + φ(n). Решаем его, учитывая что L1
= 2 (так как F1 = {0/1,
1/1}), получим:
Ln = 1 + 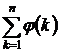
Например, L1 = 1 + φ(1) = 1 + 1 =
2, L4 = 1 + φ(1) +
φ(2) + φ(3) + φ(4) = 1 + 1 + 1 + 2 + 2 = 7.
Длина Fn приблизительно равна 3n2 / π2 ≈ 0.3039635n2.
Теорема. Для каждой пары последовательных дробей
m1 / n1 и m2 / n2 в
последовательности Fn
имеет место соотношение m2 * n1 – m1
* n2 = 1. Докажем это
равенство по индукции.
База индукции. Для пары 0/1 и
1/0 это соотношение верно: 1 * 1 – 0 * 0 = 1.
Шаг индукции. Покажем что при
вставке медианты между дробями x / y и z / t, для которых равенство yz – xt = 1 верно, оно также будет выполняться для дробей x / y и (x + z) / (y + t), а также для
дробей (x + z) / (y + t) и z / t. Действительно:
y * (x + z) – x * (y
+ t) = yz – xt = 1,
z * (y + t) – t * (x
+ z) = zy – tx = 1
Следствие. Что
означает условие yz – xt = 1? Оно означает, что НОД(x, y) = НОД(z, t) = 1, то есть x и y, z и t взаимно просты. Если предположить, что НОД(x, y) = d > 1, то выражение yz – xt делится на d и
никак не может равняться 1. Таким образом мы доказали что все получаемые
описанным образом дроби будут несократимыми.
Теорема. Медианта двух дробей всегда лежит между
ними.
Доказательство. Пусть x / y и z / t – две последовательные дроби, причем x / y < z / t (или то же самое
что xt – yz < 0). Докажем что x / y < (x + z) / (y + t) < z / t. Приведем к
общему значенателю, получим:
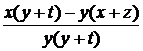 =
= 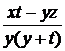 < 0,
< 0,
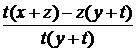 =
= 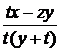 < 0
< 0
Следствие.
Все дроби последовательности Фарея упорядочены.
Множество всех
неотрицательных дробей можно построить при помощи дерева Штерна – Брокко:
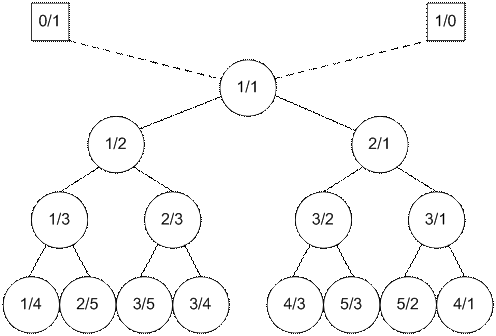
Для получения
последовательности Фарея Fn
необходимо взять множество дробей, получаемое при построении дерева
Штерна-Броко на бесконечной итерации, и оставить в нем только те дроби,
знаменатели которых не превосходят n,
а числители не превосходят знаменатели.
Рассмотрим нерекурсивную
реализацию алгоритма. Покажем, как можно сгенерировать очередной член
последовательности Фарея Fn
имея два предыдущих. Пусть a / b, c / d, p
/ q – три последовательных члена Fn. Тогда
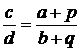
Поскольку дробь c / d несократимая,
то существует такое k что a + p
= ck, b + q = dk. Отсюда p = ck – a, q = dk – b. Вычислим разность
соседних дробей:
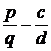 =
= ![]() =
= 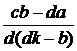
Чтобы c / d и p / q были соседними, указанная разность
должна быть наименьшей. Чем больше значение k, тем меньше
разность. Однако q = kd – b ≤ n, откуда k ≤ (n + b)
/ d. Учитывая что k целое, получим что k
= ![]() . Отсюда
. Отсюда
p = c![]() – a,
– a,
q = d![]() – b
– b
Поскольку в
последовательности Fn
первые два члена равны 0/1 и 1/n, то
последовательно сгенерировать остальные члены по указанной формуле не составит
труда.
Пример
Рассмотрим
процесс построения F5 из F4:
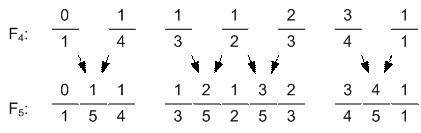
F1 = {0/1,
1/1}
F2 = {0/1,
1/2,
1/1}
F3 = {0/1, 1/3, 1/2, 2/3, 1/1}
F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1}
F5 = {0/1, 1/5, 1/4, 1/3,
2/5, 1/2, 3/5,
2/3, 3/4, 4/5, 1/1}
F6 = {0/1, 1/6, 1/5, 1/4, 1/3,
2/5, 1/2, 3/5,
2/3, 3/4, 4/5, 5/6, 1/1}
F7 = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1}
F8 = {0/1, 1/8,
1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4,
4/5, 5/6, 6/7, 7/8, 1/1}
Реализация алгоритма
Функция farey генерирует все дроби последовательности Фарея Fn, лежащие в интервале от a1 / b1 до a2
/ b2 (не включительно)
согласно следующей схеме:
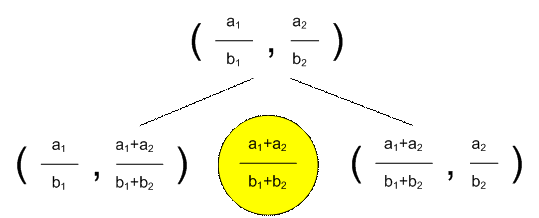
Как только будет
сгенерирована k-ая дробь, выводим ее,
устанавливаем flag = 1 и выходим из
функции.
void farey(int
a1, int b1, int
a2, int b2)
{
if (n < b1
+ b2) return;
farey(a1,b1,a1+a2,b1+b2);
if (flag) return;
if (k == 1)
{
printf("%d/%d\n",a1+a2,b1+b2);
flag = 1;
return;
}
k--;
farey(a1+a2,b1+b2,a2,b2);
}
Основная часть
программы. Генерируем все дроби из Fn,
начиная с интервала (0/1, 1/1). Как только будет сгенерирована k-ая дробь, выводим ее и останавливаем дальнейший
процесс генерации. Если по окончанию работы функции farey flag = 0, то это означает, что k-ой
дробью является 1/1.
while(scanf("%d
%d",&n,&k) == 2)
{
flag = 0; farey(0,1,1,1);
if (!flag)
printf("1/1\n");
}
Реализация алгоритма - итеративная
#include <stdio.h>
int i, n, k;
int a, b, c, d, p, q;
int main(void)
{
while(scanf("%d %d",&n,&k) == 2)
{
a = 0; b = 1; //
0 / 1
c = 1; d = n; //
1 / n
p = c; q = d;
for(i = 1;
i < k; i++)
{
p = c * ((n + b) / d) - a;
q = d * ((n + b) / d) - b;
a = c; b = d;
c = p; d = q;
}
printf("%d/%d\n",p,q);
}
return 0;
}